��Ŀ����
��������˵������ȷ���� ���١���am2��bm2����a��b����������Ϊ�棻
�����Իع鷽�̶�Ӧ��ֱ��
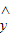 =
=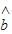 x+
x+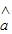 һ���������������ݵ� ��x1��y1������x2��y2����������xn��yn���е�һ���㣻
һ���������������ݵ� ��x1��y1������x2��y2����������xn��yn���е�һ���㣻����ʵ��x��y��[0��1]�������㣺x2+y2��1�ĸ���Ϊ
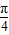 ��
��������ѧ���ɷ�֤����n+1����n+2������n+n��=2n•1•3����2n-1����n��N*��ʱ���ӡ�k������k+1����֤���������������һ����ʽ��2��2k+1����
���𰸡�����������д���������⣬Ȼ�����ж��Ƿ���ȷ��
�����Իع鷽�̶�Ӧ��ֱ��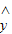 =
= x+
x+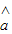 ������С���˷���������ģ���һ���������������ݵ㣻
������С���˷���������ģ���һ���������������ݵ㣻
�۱�����һ�����θ��ͣ����鷢���������¼���Ӧ�ļ����Ǧ�={��x��y��|-1��x��1��-1��y��1}�������������¼���Ӧ�ļ�����A={��x��y��|-1��x��1��-1��y��1��x2+y2��1}�������������϶�Ӧ��ͼ�ε���������ݼ��θ����ʹ�ʽ�õ������
�ܸ��ݡ�k������k+1��ʱ����ʽ�����������2k+1��2k+2��ͬʱ����һ��k+1�����жϢ۵���٣�
����⣺�١���am2��bm2����a��b����������Ϊ����a��b����am2��bm2����m=0����a=b���ʢٴ���
�ڣ����Իع鷽�̶�Ӧ��ֱ�� =
= x+
x+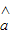 һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е����ĵ㣬��һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е�һ���㣬�ʴ���
һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е����ĵ㣬��һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е�һ���㣬�ʴ���
��������֪������һ�����θ��ͣ�
���鷢���������¼���Ӧ�ļ����Ǧ�={��x��y��|0��x��1��0��y��1}��
���������1×1=1��
�����������¼���Ӧ�ļ�����A={��x��y��|0��x��1��0��y��1��x2+y2��1}
����A��Ӧ��ͼ�ε�����DZ߳�Ϊ1���������ڲ�����Բ���ⲿ�������1-
����ݼ��θ��͵ĸ��ʹ�ʽ�õ�P=1- ���ʲ���ȷ��
���ʲ���ȷ��
������ѧ���ɷ�֤����n+1����n+2������n+n��=2n•1•3����2n-1����n��N*��ʱ���ӡ�k������k+1����֤ ���������������һ����ʽ��2��2k+1�����ʢ���ȷ��
�ʴ�Ϊ����
������������Ҫ����������ٵ��ж������⿼���֪ʶ�������������ж���Ӧ�ã������������ռ��θ��ͣ����Իع鷽�̣���ѧ���ɷ���֤������Ȼ���֪ʶ���ǽ����Ĺؼ���
�����Իع鷽�̶�Ӧ��ֱ��
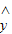 =
= x+
x+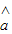 ������С���˷���������ģ���һ���������������ݵ㣻
������С���˷���������ģ���һ���������������ݵ㣻�۱�����һ�����θ��ͣ����鷢���������¼���Ӧ�ļ����Ǧ�={��x��y��|-1��x��1��-1��y��1}�������������¼���Ӧ�ļ�����A={��x��y��|-1��x��1��-1��y��1��x2+y2��1}�������������϶�Ӧ��ͼ�ε���������ݼ��θ����ʹ�ʽ�õ������
�ܸ��ݡ�k������k+1��ʱ����ʽ�����������2k+1��2k+2��ͬʱ����һ��k+1�����жϢ۵���٣�
����⣺�١���am2��bm2����a��b����������Ϊ����a��b����am2��bm2����m=0����a=b���ʢٴ���
�ڣ����Իع鷽�̶�Ӧ��ֱ��
 =
= x+
x+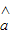 һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е����ĵ㣬��һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е�һ���㣬�ʴ���
һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е����ĵ㣬��һ���������������ݵ� ��x1-y1������x2-y2����������xn��yn���е�һ���㣬�ʴ�����������֪������һ�����θ��ͣ�
���鷢���������¼���Ӧ�ļ����Ǧ�={��x��y��|0��x��1��0��y��1}��
���������1×1=1��
�����������¼���Ӧ�ļ�����A={��x��y��|0��x��1��0��y��1��x2+y2��1}
����A��Ӧ��ͼ�ε�����DZ߳�Ϊ1���������ڲ�����Բ���ⲿ�������1-

����ݼ��θ��͵ĸ��ʹ�ʽ�õ�P=1-
 ���ʲ���ȷ��
���ʲ���ȷ��������ѧ���ɷ�֤����n+1����n+2������n+n��=2n•1•3����2n-1����n��N*��ʱ���ӡ�k������k+1����֤ ���������������һ����ʽ��2��2k+1�����ʢ���ȷ��
�ʴ�Ϊ����
������������Ҫ����������ٵ��ж������⿼���֪ʶ�������������ж���Ӧ�ã������������ռ��θ��ͣ����Իع鷽�̣���ѧ���ɷ���֤������Ȼ���֪ʶ���ǽ����Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
��֪x��y��zΪ����ʵ��������ʽ
+
+
+
��ֵ����ɵļ���ΪM������������˵������ȷ���ǣ�������
| x |
| |x| |
| y |
| |y| |
| z |
| |z| |
| xyz |
| |xyz| |
| A��0∉M | B��2��M |
| C��-4∉M | D��4��M |
 ��ֵ����ɵļ���ΪM������������˵������ȷ���ǣ� ��
��ֵ����ɵļ���ΪM������������˵������ȷ���ǣ� ��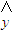 =
=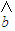 x+
x+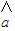 һ���������������ݵ� ��x1��y1������x2��y2����������xn��yn���е�һ���㣻
һ���������������ݵ� ��x1��y1������x2��y2����������xn��yn���е�һ���㣻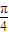 ��
��