题目内容
(21)已知数列{xn}、{yn}满足x1=x2=1,y1=y2=2,并且(Ⅰ)若x1、x3、x5成等比数列,求参数![]() 的值;
的值;
(Ⅱ)当![]() >0时,证明
>0时,证明![]() (n∈N*);
(n∈N*);
(Ⅲ)当![]() >1时,证明
>1时,证明![]() <
<![]() (n∈N*).
(n∈N*).
本小题以数列的递推关系为载体,主要考查等比数列的等比中项及前n项和公式、不等式的性质及证明等基础知识,考查运算能力和推理论证能力.
(Ⅰ)解:由已知x1=x2=1,且
![]()
若x1、x3、x5成等比数列,则![]() =x1x5,即
=x1x5,即![]() 2=
2=![]() 6.而
6.而![]() ≠0,解得
≠0,解得![]() =±1.
=±1.
(Ⅱ)证明:由已知,![]() >0,x1=x2=1及y1=y2=2,可得xn>0,yn>0.由不等式的性质,有
>0,x1=x2=1及y1=y2=2,可得xn>0,yn>0.由不等式的性质,有
![]() ≥
≥![]()
![]() ≥
≥![]() 2
2![]() ≥…≥
≥…≥![]() n-1
n-1![]() =
=![]() n-1。
n-1。
另一方面,
![]()
因此,![]() (n∈N*).故
(n∈N*).故
![]()
![]() (n∈N*).
(n∈N*).
(Ⅲ)证明:当![]() >1时,由(Ⅱ)可知yn>xn≥1(n∈N*)。
>1时,由(Ⅱ)可知yn>xn≥1(n∈N*)。
又由(Ⅱ)![]()
![]() (n∈N*),则
(n∈N*),则
![]()
![]() ,
,
从而![]()
![]() =
=![]() n-1(n∈N*).因此
n-1(n∈N*).因此
![]()
≤1+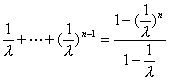 <
<![]() .
.

练习册系列答案
相关题目
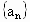 、
、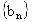 与函数f(x)、g(x),x
与函数f(x)、g(x),x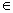 R满足条件:
R满足条件: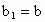 ,
,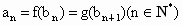 .
.
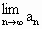 存在,求t的取值范围,并求
存在,求t的取值范围,并求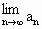 (用t表示);
(用t表示);
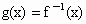 ,b=1,f(1)<1,证明对任意的
,b=1,f(1)<1,证明对任意的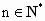 ,
,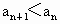 .
.