题目内容
已知函数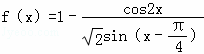 .
.
(Ⅰ)求函数f(x)的定义域;
(Ⅱ)求函数f(x)的单调增区间.
考点:
二倍角的余弦;正弦函数的定义域和值域;正弦函数的单调性.
专题:
三角函数的图像与性质.
分析:
(Ⅰ)由分母不为0,得到sin(x﹣![]() )≠0,利用正弦函数的性质即可求出函数f(x)的定义域;
)≠0,利用正弦函数的性质即可求出函数f(x)的定义域;
(Ⅱ)函数解析式第二项分子利用二倍角的余弦函数公式化简,第二项利用两角和与差的正弦函数公式化简,约分后再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的单调性即可求出函数的单调递增区间.
解答:
解:(I)∵sin(x﹣![]() )≠0,
)≠0,
∴x﹣![]() ≠kπ,k∈Z,
≠kπ,k∈Z,
则函数的定义域为{x|x≠kπ+![]() ,k∈Z};
,k∈Z};
(II)∵f(x)=1﹣![]() =1+(cosx+sinx)=1+sinx+cosx=1+
=1+(cosx+sinx)=1+sinx+cosx=1+![]() sin(x+
sin(x+![]() ),
),
又∵y=sinx的单调递增区间为(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z,
),k∈Z,
令2kπ﹣![]() <x+
<x+![]() <2kπ+
<2kπ+![]() ,
,
解得:2kπ﹣![]() <x<2kπ+
<x<2kπ+![]() ,
,
又注意到x≠kπ+![]() ,
,
则f(x)的单调递增区间为(2kπ﹣![]() ,2kπ+
,2kπ+![]() ),k∈Z.
),k∈Z.
点评:
此题考查了二倍角的余弦函数公式,正弦函数的定义域和值域,以及正弦函数的单调性,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
.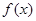 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求