题目内容
.(本题满分12分)
给定椭圆 >
> >0
>0 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为 的圆是椭圆
的圆是椭圆 的“伴随圆”.若椭圆
的“伴随圆”.若椭圆 的一个焦点为
的一个焦点为 ,其短轴上的一个端点到
,其短轴上的一个端点到 的距离为
的距离为 .
.
(1)求椭圆 的方程及其“伴随圆”方程;
的方程及其“伴随圆”方程;
(2)若倾斜角为 的直线
的直线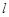 与椭圆C只有一个公共点,且与椭圆
与椭圆C只有一个公共点,且与椭圆 的“伴随圆”相交于M、N两点,求弦MN的长;
的“伴随圆”相交于M、N两点,求弦MN的长;
(3)点 是椭圆
是椭圆 的“伴随圆”上的一个动点,过点
的“伴随圆”上的一个动点,过点 作直线
作直线 ,使得
,使得 与椭圆
与椭圆 都只有一个公共点,求证:
都只有一个公共点,求证: 。
。
【答案】
(1)因为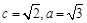 ,所以
,所以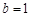
所以椭圆的方程为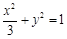 ,伴随圆方程
,伴随圆方程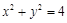 ……………2分
……………2分
(2)设直线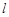 的方程
的方程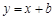 ,由
,由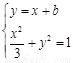 得
得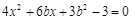
由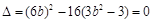 得
得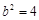
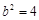
圆心到直线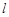 的距离为
的距离为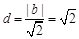 所以
所以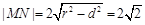 ………………………………………6分
………………………………………6分
(3)①当 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设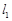 无斜率,
无斜率,
因为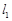 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为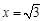 或
或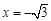 ,
,
当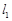 方程为
方程为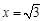 时,此时
时,此时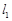 与伴随圆交于点
与伴随圆交于点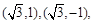
此时经过点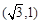 (或
(或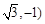 且与椭圆只有一个公共点的直线是
且与椭圆只有一个公共点的直线是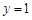
(或 ,即
,即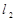 为
为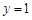 (或
(或 ,显然直线
,显然直线 垂直;
垂直;
同理可证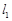 方程为
方程为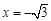 时,直线
时,直线 垂直……………………7分
垂直……………………7分
②当 都有斜率时,设点
都有斜率时,设点 其中
其中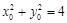 ,
,
 设经过点
设经过点 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为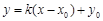 ,
,
 由
由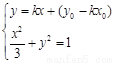 ,消去
,消去 得到
得到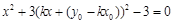 ,
,
即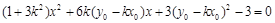 ,……………8分
,……………8分
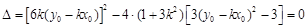 ,
,
经过化简得到: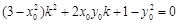 ,
,
因为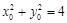 ,所以有
,所以有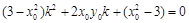 ,…………………………10分
,…………………………10分
设 的斜率分别为
的斜率分别为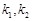 ,因为
,因为 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以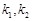 满足方程
满足方程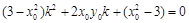 ,
,
因而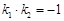 ,即
,即 垂直.………………………………………………12分
垂直.………………………………………………12分
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面