题目内容
设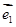 与
与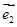 是两个不共线的向量,已知
是两个不共线的向量,已知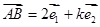 ,
,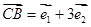 ,
,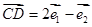 ,则当
,则当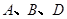 三点共线时,
三点共线时,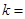 .
.
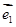 与
与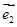 是两个不共线的向量,已知
是两个不共线的向量,已知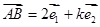 ,
,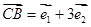 ,
,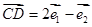 ,则当
,则当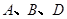 三点共线时,
三点共线时,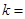 .
. 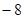
解:∵A,B,D三点共线,∴ AB 与 BD 共线,
∴存在实数λ,使得 AB =λ BD ;
∵ BD =" CD" - CB ="2" e1 - e2 -( e1 +3 e2)= e1 -4 e2,
∴2 e1 +k e2 =λ( e1 -4 e2),
∵ e 1, e 2是平面内不共线的两向量,
∴ 2=λ k=-4λ 解得k=-8.
故答案为:-8
∴存在实数λ,使得 AB =λ BD ;
∵ BD =" CD" - CB ="2" e1 - e2 -( e1 +3 e2)= e1 -4 e2,
∴2 e1 +k e2 =λ( e1 -4 e2),
∵ e 1, e 2是平面内不共线的两向量,
∴ 2=λ k=-4λ 解得k=-8.
故答案为:-8

练习册系列答案
相关题目
 =(1,-3),
=(1,-3),  =(-2,4),
=(-2,4),  =(-1,-2),若表示向量4
=(-1,-2),若表示向量4 的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量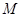 在平面
在平面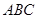 内,并且对空间任一点
内,并且对空间任一点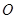 ,
,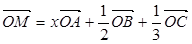 则
则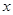 的值为 ( )
的值为 ( )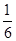
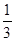
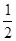

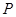 是
是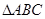 内任意一点,
内任意一点, 表示
表示
 ,定义
,定义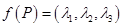 ,已知
,已知 ,
,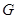 是
是 在
在 内
内 内
内  内
内 ,
,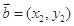 ,下列叙述错误的是( )
,下列叙述错误的是( )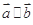 ,则
,则
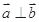 ,则
,则
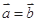 ,则
,则
 ,则
,则
 ,
,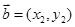 ,若
,若 ,
,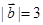 ,
, ,则
,则 ()
()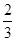

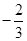

 的夹角为( )
的夹角为( )



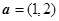 ,
,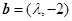 .若
.若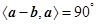 ,则实数
,则实数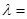 _____.
_____.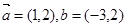 ,若
,若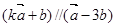 ,则实数k的取值为 ▲ 。
,则实数k的取值为 ▲ 。