题目内容
3.若抛物线x2=12y与双曲线$\frac{x^2}{k}+\frac{y^2}{5}=1$有相同的焦点,则双曲线的离心率为$\frac{{3\sqrt{5}}}{5}$.分析 利用抛物线的方程先求出抛物线的焦点即双曲线的焦点,利用双曲线的方程与系数的关系,即可得出结论.
解答 解:抛物线x2=12y的焦点坐标为(0,3),
∵抛物线x2=12y与双曲线$\frac{x^2}{k}+\frac{y^2}{5}=1$有相同的焦点,
∴5-k=9,
∴k=-4,
双曲线$\frac{x^2}{k}+\frac{y^2}{5}=1$中a=$\sqrt{5}$,b=2,c=3,离心率e=$\frac{c}{a}$=$\frac{{3\sqrt{5}}}{5}$.
故答案为:$\frac{{3\sqrt{5}}}{5}$.
点评 本题考查双曲线的抛物线的性质,简单题,注意三参数的关系:c2=a2+b2.

练习册系列答案
相关题目
18.若x>0,y>0,x+2y+2xy=8,则x+2y的最小值是( )
| A. | $\frac{11}{2}$ | B. | 3 | C. | $\frac{9}{2}$ | D. | 4 |
15.复数z满足z(3-4i)=1(i是虚数单位),则|z|=( )
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{25}$ | C. | $\frac{1}{25}$ | D. | $\frac{1}{5}$ |
12.在极坐标系中,设点A为曲线C:ρ=2θ在极轴Ox上方的一点,且0≤AOx≤$\frac{π}{4}$,以A为直角顶点,AO为一条直角边作等腰直角三角形OAB(B在A的右下方),求点B的轨迹方程.
13.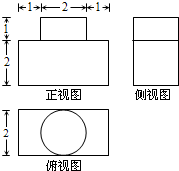 如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )
如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )
 如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )
如图,已知某品牌墨水瓶的外形三视图和尺寸,则该墨水瓶的容积为(瓶壁厚度忽略不计)( )| A. | 8+π | B. | 8+4π | C. | 16+π | D. | 16+4π |
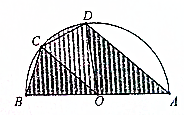 如图,有一景区的平面图是一半圆形,其中AB长为2km,C、D两点在半圆弧上,满足BC=CD,设∠COB=θ.
如图,有一景区的平面图是一半圆形,其中AB长为2km,C、D两点在半圆弧上,满足BC=CD,设∠COB=θ.