题目内容
已知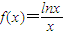 .
.(I)讨论f(x)的单调性,并求出f(x)的最大值;
(II)求证:
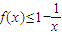 ;
;(III)比较f(22)+f(32)+…f(n2)与
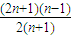 的大小,并证明你的结论.
的大小,并证明你的结论.
【答案】分析:对于(I)讨论f(x)的单调性,求f(x)的最大值问题,可先求出函数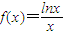 的导函数,根据导函数的零点讨论极值,根据导函数的大于零或小于零,讨论函数的单调性问题.
的导函数,根据导函数的零点讨论极值,根据导函数的大于零或小于零,讨论函数的单调性问题.
对于(II)求证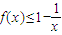 ,可以考虑把
,可以考虑把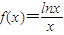 代入移向转化为考查函数g(x)=lnx-x+1≤0的问题,再根据导函数求极值的方法证得即可.
代入移向转化为考查函数g(x)=lnx-x+1≤0的问题,再根据导函数求极值的方法证得即可.
对于(III)比较f(22)+f(32)+…f(n2)与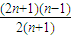 的大小,分析由(2)证得
的大小,分析由(2)证得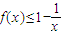 ,从而
,从而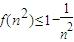 ,故可求出f(22)+f(32)+…f(n2)的小于等于一个关于n的式子.再根据
,故可求出f(22)+f(32)+…f(n2)的小于等于一个关于n的式子.再根据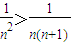 化简即可证得大小.
化简即可证得大小.
解答:解:(I)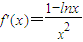 ,
,
令f'(x)>0,得x<e,令f'(x)<0得x>e.
又f(x)的定义域为(0,+∞),∴f(x)在(0,e)上递增,在(e,+∞)递减,
从而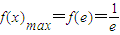 .
.
(II)要证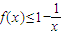 即证
即证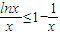 ,
,
∵x>0,∴只需证:lnx-x+1≤0.
令g(x)=lnx-x+1,则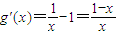 ,
,
令g'(x)>0,得0<x<1,g'(x)<0得x>1(x<0舍去).
∴g(x)在(0,1)上递增,在(1,+∞)上递减,
∴g(x)≤g(1)=0,∴lnx-x+1≤0成立,
即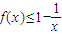 成立.
成立.
(III)由(2)知,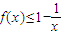 ,从而
,从而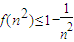 ,
,
∴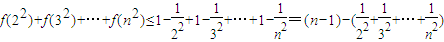 .
.
又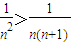 ,
,
∴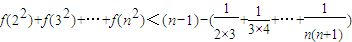 =
=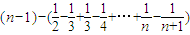 =
=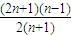 ,
,
即答案为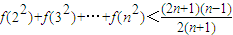 .
.
点评:此题主要考查函数单调性和极值的求法问题,其中涉及到由导函数求函数极值知识点,此类知识点属于高考重点常考题型,综合性强,计算大,易错同学们需要多加注意.
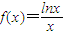 的导函数,根据导函数的零点讨论极值,根据导函数的大于零或小于零,讨论函数的单调性问题.
的导函数,根据导函数的零点讨论极值,根据导函数的大于零或小于零,讨论函数的单调性问题.对于(II)求证
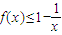 ,可以考虑把
,可以考虑把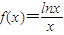 代入移向转化为考查函数g(x)=lnx-x+1≤0的问题,再根据导函数求极值的方法证得即可.
代入移向转化为考查函数g(x)=lnx-x+1≤0的问题,再根据导函数求极值的方法证得即可.对于(III)比较f(22)+f(32)+…f(n2)与
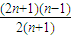 的大小,分析由(2)证得
的大小,分析由(2)证得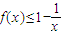 ,从而
,从而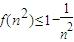 ,故可求出f(22)+f(32)+…f(n2)的小于等于一个关于n的式子.再根据
,故可求出f(22)+f(32)+…f(n2)的小于等于一个关于n的式子.再根据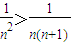 化简即可证得大小.
化简即可证得大小.解答:解:(I)
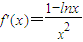 ,
,令f'(x)>0,得x<e,令f'(x)<0得x>e.
又f(x)的定义域为(0,+∞),∴f(x)在(0,e)上递增,在(e,+∞)递减,
从而
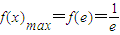 .
.(II)要证
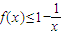 即证
即证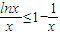 ,
,∵x>0,∴只需证:lnx-x+1≤0.
令g(x)=lnx-x+1,则
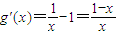 ,
,令g'(x)>0,得0<x<1,g'(x)<0得x>1(x<0舍去).
∴g(x)在(0,1)上递增,在(1,+∞)上递减,
∴g(x)≤g(1)=0,∴lnx-x+1≤0成立,
即
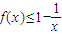 成立.
成立.(III)由(2)知,
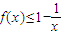 ,从而
,从而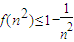 ,
,∴
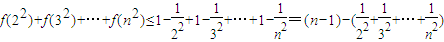 .
.又
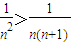 ,
,∴
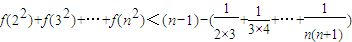 =
=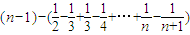 =
=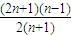 ,
,即答案为
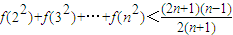 .
.点评:此题主要考查函数单调性和极值的求法问题,其中涉及到由导函数求函数极值知识点,此类知识点属于高考重点常考题型,综合性强,计算大,易错同学们需要多加注意.

练习册系列答案
相关题目
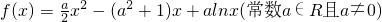
 与a的大小.
与a的大小.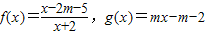 ,
,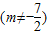
 ,
,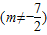
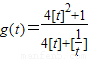 的最小值.
的最小值.