题目内容
若存在实数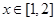
满足
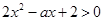，则实数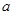
的取值范围是 ．
解析试题分析：令f（x）=
，若存在实数x∈[1，2]满足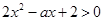，则f（1）＞0或f（2）＞0，即4-a＞0或10-2a＞0，即a＜4或a＜5，故a＜5，即实数a的取值范围是（-∞，5）
考点：本题考查了函数图象的运用
点评：构造函数，将存在性问题转化为不等式问题是解答的关键
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
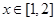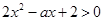若存在实数满足，则实数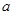的取值范围是 ．
解析试题分析：令f（x）=，若存在实数x∈[1，2]满足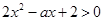，则f（1）＞0或f（2）＞0，即4-a＞0或10-2a＞0，即a＜4或a＜5，故a＜5，即实数a的取值范围是（-∞，5）
考点：本题考查了函数图象的运用
点评：构造函数，将存在性问题转化为不等式问题是解答的关键
名校课堂系列答案
的解集是________________ 
的不等式
的解集为（2，
），则
的解集为 ．
的解集是 . 
＞0对
恒成立，则x的取值范围是__________. 
的解集是 
上恒成立，则实数a的取值范围是 . 
的定义域为集合A，关于x的不等式
的解集为B，求使
的取值范围．
的不等式
解集为
，则
的取值范围是____________；