题目内容
 一次函数f(x)=mx+n与指数型函数g(x)=ax+b(a>0,a≠1)的图象交于两点A(0,1),B(1,2),解答下列各题:
一次函数f(x)=mx+n与指数型函数g(x)=ax+b(a>0,a≠1)的图象交于两点A(0,1),B(1,2),解答下列各题:(1)求一次函数f(x)和指数型函数g(x)的表达式;
(2)作出这两个函数的图象;
(3)填空:当x∈
[0,1]
[0,1]
时,f(x)≥g(x);当x∈(-∞,0)∪(1,+∞)
(-∞,0)∪(1,+∞)
时,f(x)<g(x).分析:(1)把点A、B的坐标代入函数解析式,得方程组,解方程组即可
(2)根据函数解析式和函数的性质,做出函数图象
(3)由条件和(2)可得答案
(2)根据函数解析式和函数的性质,做出函数图象
(3)由条件和(2)可得答案
解答:解:(1)因为两个函数的图象交于两点A(0,1),B(1,2)
所以有
,
解得m=n=1,a=2,b=0所以两个函数的表达式为f(x)=x+1,g(x)=2x
(2)如图所示,为所画函数图象
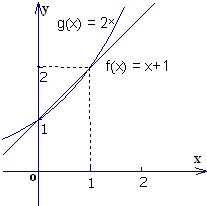
(3)由图象知,当x∈[0,1]时,f(x)≥g(x);当x∈(-∞,0)∪(1,+∞)时,f(x)<g(x)
故答案为:[0,1];(-∞,0)∪(1,+∞)
所以有
|
|
解得m=n=1,a=2,b=0所以两个函数的表达式为f(x)=x+1,g(x)=2x
(2)如图所示,为所画函数图象

(3)由图象知,当x∈[0,1]时,f(x)≥g(x);当x∈(-∞,0)∪(1,+∞)时,f(x)<g(x)
故答案为:[0,1];(-∞,0)∪(1,+∞)
点评:本题考查用待定系数法求函数解析式,及函数的图象和性质.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目