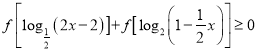Question

【题目】如图，有一个正三棱锥的零件，P是侧面ACD上的一点．

过点P作一个与棱AB垂直的截面，怎样画法？并说明理由．

Answer 1

【答案】详见解析．

【解析】试题分析：取 中点 ，可利用直线与平面垂直的判定定理，可证得 平面 ，过点与平行的直线与平面，进而与 垂直。

(方法一)

画法：过点P在面ACD内作EF//CD，交AC于E点，交AD于F点．

过E作EG⊥AB，连接FG，平面EFG为所求．

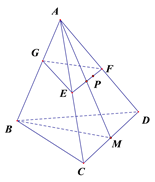理由：取CD中点M，连接AM，BM．

∵A-BCD为正三棱锥,

∴AC=AD，BC=BD,

∴BM⊥CD，AM⊥CD ,

AM∩BM=M,

AM平面ABM ,BM平面ABM,

∴CD⊥平面ABM ．

∵AB平面ABM,

∴CD⊥AB．

∵EF∥CD,

∴EF⊥AB ．

过E作EG⊥AB，连接FG,

∵EF∩EG=E ．

EF面EFG，EG面EFG,

AB⊥面EFG ．

（方法二）

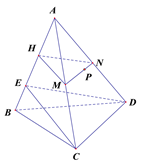
画法：过C在平面ABC内M作CE⊥AB，垂足为E．连接DE．

过点P作MN // CD，交AC于M，AD于N．

过M作MH//CE，交AE于H，连接HN，平面HMN为所求．

理由：,

．

,,

,

,

．

由画法知， AB⊥HM，

∵HM∩HN=H,

HM面MNH，HN面MNH,

．