题目内容
在极坐标系中,已知圆C的圆心C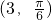 ,半径r=1,Q点在圆C上运动.
,半径r=1,Q点在圆C上运动.
(1)求圆C的极坐标方程;
(2)若P在直线OQ上运动,且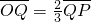 ,求动点P轨迹的极坐标方程.
,求动点P轨迹的极坐标方程.
解:(1)将圆心C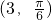 ,化成直角坐标为(
,化成直角坐标为( ,
, ),半径R=1,(2分)
),半径R=1,(2分)
故圆C的方程为(x- )2+(y-
)2+(y- )2=1.(4分)
)2=1.(4分)
再将C化成极坐标方程,得(ρcosθ- )2+(ρsinθ-
)2+(ρsinθ- )2=1.(6分)
)2=1.(6分)
化简,得 -8.
-8.
此即为所求的圆C的方程.(10分)
(2)由OQ:QP=2:3,得OQ:OP=2:5.
所以点P的参数方程为: .
.
即
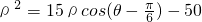 .
.
分析:(1)先利用圆心坐标与半径求得圆的直角坐标方程,再利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得圆C的极坐标方程.
(2)由OQ:QP=2:3,得OQ:OP=2:5.从而得到点P的参数方程 .下面利用三角函数的和角公式化简即可.
.下面利用三角函数的和角公式化简即可.
点评:本题考查点的极坐标和直角坐标的互化,即利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即可.
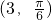 ,化成直角坐标为(
,化成直角坐标为( ,
, ),半径R=1,(2分)
),半径R=1,(2分)故圆C的方程为(x-
 )2+(y-
)2+(y- )2=1.(4分)
)2=1.(4分)再将C化成极坐标方程,得(ρcosθ-
 )2+(ρsinθ-
)2+(ρsinθ- )2=1.(6分)
)2=1.(6分)化简,得
 -8.
-8.此即为所求的圆C的方程.(10分)
(2)由OQ:QP=2:3,得OQ:OP=2:5.
所以点P的参数方程为:
 .
.即

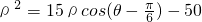 .
.分析:(1)先利用圆心坐标与半径求得圆的直角坐标方程,再利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得圆C的极坐标方程.
(2)由OQ:QP=2:3,得OQ:OP=2:5.从而得到点P的参数方程
 .下面利用三角函数的和角公式化简即可.
.下面利用三角函数的和角公式化简即可.点评:本题考查点的极坐标和直角坐标的互化,即利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即可.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目