题目内容
已知f(x)=loga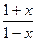 (a>0且a≠1).
(a>0且a≠1).
(1)求函数的定义域;
(2)讨论函数的单调性;
(3)求使f(x)>0的x的取值范围.
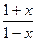 (a>0且a≠1).
(a>0且a≠1).(1)求函数的定义域;
(2)讨论函数的单调性;
(3)求使f(x)>0的x的取值范围.
(1)由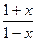 >0得-1<x<1.
>0得-1<x<1.
∴函数的定义域为(-1,1).
(2)对任意-1<x1<x2<1,
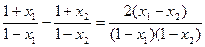 <0,∴
<0,∴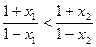 .
.
当a>1时,loga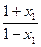 <log a
<log a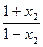 ,即f(x1)<f(x2);
,即f(x1)<f(x2);
当0<a<1时,loga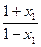 >loga
>loga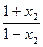 ,即f(x1)>f(x2).
,即f(x1)>f(x2).
∴当a>1时,f(x)为(-1,1)上的增函数;
当0<a<1时,f(x)为(-1,1)上的减函数.
(3)loga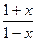 >0=loga1.
>0=loga1.
当a>1时,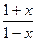 >1,即
>1,即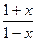 -1=
-1=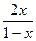 >0.
>0.
∴2x(x-1)<0.∴0<x<1.
当0<a<1时,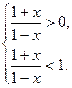 解得-1<x<0.
解得-1<x<0.
∴当a>1时,f(x)>0的解为(0,1);
当0<a<1时,f(x)>0的解为(-1,0).
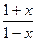 >0得-1<x<1.
>0得-1<x<1.∴函数的定义域为(-1,1).
(2)对任意-1<x1<x2<1,
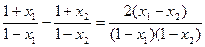 <0,∴
<0,∴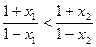 .
.当a>1时,loga
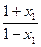 <log a
<log a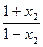 ,即f(x1)<f(x2);
,即f(x1)<f(x2);当0<a<1时,loga
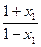 >loga
>loga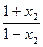 ,即f(x1)>f(x2).
,即f(x1)>f(x2).∴当a>1时,f(x)为(-1,1)上的增函数;
当0<a<1时,f(x)为(-1,1)上的减函数.
(3)loga
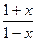 >0=loga1.
>0=loga1.当a>1时,
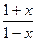 >1,即
>1,即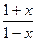 -1=
-1=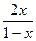 >0.
>0.∴2x(x-1)<0.∴0<x<1.
当0<a<1时,
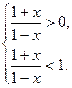 解得-1<x<0.
解得-1<x<0.∴当a>1时,f(x)>0的解为(0,1);
当0<a<1时,f(x)>0的解为(-1,0).
注意对数函数的底和真数的制约条件以及底的取值范围对单调性的影响.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, ,
, ,
,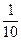 时所对应的图象,则相应于C1,C2,C3,C4的a的值依次是( )
时所对应的图象,则相应于C1,C2,C3,C4的a的值依次是( )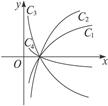
 ,且
,且 求实数
求实数 的取值范围.
的取值范围.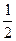 <1,那么a的取值范围是( )
<1,那么a的取值范围是( )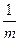 ,则x的值为( )
,则x的值为( )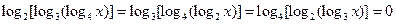 ,则
,则 ( )
( )


