题目内容
设α是空间中的一个平面，l，m，n是三条不同的直线，
①若m?α，n?α，l⊥m，l⊥n，则l⊥α；
②若l∥m，m∥n，l⊥α，则n⊥α；
③若l∥m，m⊥α，n⊥α，则l∥n；
④若m?α，n⊥α，l⊥n，则l∥m；
则上述命题中正确的是（ ）
①若m?α，n?α，l⊥m，l⊥n，则l⊥α；
②若l∥m，m∥n，l⊥α，则n⊥α；
③若l∥m，m⊥α，n⊥α，则l∥n；
④若m?α，n⊥α，l⊥n，则l∥m；
则上述命题中正确的是（ ）
分析：①根据线面垂直的判定，可判断；
②根据平行线的传递性，可得l∥n，故l⊥α时，一定有n⊥α；
③由垂直于同一平面的两直线平行得m∥n，再根据平行线的传递性，即可得l∥n；
④m?α，n⊥α，则n⊥m，根据l⊥n，可得l，m平行、相交、异面都有可能．
②根据平行线的传递性，可得l∥n，故l⊥α时，一定有n⊥α；
③由垂直于同一平面的两直线平行得m∥n，再根据平行线的传递性，即可得l∥n；
④m?α，n⊥α，则n⊥m，根据l⊥n，可得l，m平行、相交、异面都有可能．
解答：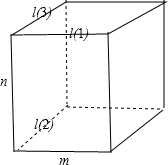
解：①根据线面垂直的判定，当m，n相交时，结论成立，故①不正确；
②根据平行线的传递性，可得l∥n，故l⊥α时，一定有n⊥α，故②正确；
③由垂直于同一平面的两直线平行得m∥n，再根据平行线的传递性，即可得l∥n，故③正确．
④m?α，n⊥α，则n⊥m，∵l⊥n，∴可以选用正方体模型，可得l，m平行、相交、异面都有可能，如图所示，故④不正确
故正确的命题是②③
故选B．
解：①根据线面垂直的判定，当m，n相交时，结论成立，故①不正确；②根据平行线的传递性，可得l∥n，故l⊥α时，一定有n⊥α，故②正确；
③由垂直于同一平面的两直线平行得m∥n，再根据平行线的传递性，即可得l∥n，故③正确．
④m?α，n⊥α，则n⊥m，∵l⊥n，∴可以选用正方体模型，可得l，m平行、相交、异面都有可能，如图所示，故④不正确
故正确的命题是②③
故选B．
点评：本题考查空间中直线与直线、平面之间的位置关系，熟练掌握理解空间中线与线，线与面，面与面的位置关系及判定定理及较好的空间想像能力是准确解答此类题目的关键．
练习册系列答案
相关题目