题目内容
(本题满分14分)数列![]() 是首项为
是首项为![]() ,公差为
,公差为![]() 的等差数列,若数列
的等差数列,若数列![]() 中任意不同的两项之和仍是该数列的一项,则称该数列是“封闭数列”
中任意不同的两项之和仍是该数列的一项,则称该数列是“封闭数列”
(1)试写出一个不是“封闭数列”的等差数列的通项公式,并说明理由;
(2)求证:数列![]() 为“封闭数列”的充分必要条件是存在整数
为“封闭数列”的充分必要条件是存在整数![]() ,使
,使![]() 。
。
解(1)如数列![]() 不是“封闭数列”,---1分
不是“封闭数列”,---1分
![]() , -------------------2分
, -------------------2分
依题,![]() ,使
,使![]() --------------3分
--------------3分
即![]() , --------------4分
, --------------4分
这与![]() 矛盾
矛盾
所以数列![]() 不是封闭数列;--------------5分
不是封闭数列;--------------5分
法二:数列![]() 不是“封闭数列” ---1分
不是“封闭数列” ---1分
对任意的![]()
![]() ,有
,有
![]() -------------------2分
-------------------2分
依题,![]() ,使
,使 ![]() --------------3分
--------------3分
即![]()
得![]() -------------4分
-------------4分
![]() ,
,![]() ,而
,而![]() ,矛盾
,矛盾
所以数列![]() 不是封闭数列; ------------5分
不是封闭数列; ------------5分
(只要写出的通项公式能满足存在整数![]() ,使
,使![]() ,就不合)
,就不合)
(2)证明:(充分性)若存在整数![]() ,使
,使![]() ,则任取等差数列的两项
,则任取等差数列的两项![]() ,于是
,于是
![]() --------2分
--------2分
由于![]() 为正整数, -------------------3分
为正整数, -------------------3分
![]()
![]() ,
,![]() 是封闭数列 -- ----4分
是封闭数列 -- ----4分
(必要性)任取等差数列的两项![]() ,若存在
,若存在![]() 使
使![]() ,
,
则![]() --------------------6分
--------------------6分
故存在![]() ,使
,使![]() , --------------------7分
, --------------------7分
下面证明![]() 。
。
当![]() 时,显然成立。 --------------------8分
时,显然成立。 --------------------8分
对![]() ,若
,若![]() ,则取
,则取![]() ,对不同的两项
,对不同的两项![]() 和
和![]() ,存在
,存在![]() 使
使![]() +
+![]() =
=![]() ,
,
即![]()
![]() ,这与
,这与![]() 矛盾,
矛盾,
故存在整数![]() ,使
,使![]() 。 --------------------------9分
。 --------------------------9分

 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案(本题满分14分) 某中学为了解学生的睡眠情况与学习效率的关系,从中抽取20名学生作为样本进行调查.调查的数据整理分组如下表示:
|
睡眠时间(单位:小时) |
|
|
|
|
|
|
|
频 数 |
1 |
3 |
|
6 |
4 |
|
|
频 率 |
|
|
0.20 |
|
|
|
(1)将以上表格补充完整,

(2)在给定的坐标系内画出样本的频率分布直方图;
(3)为了比较睡眠情况与学习效率的关系,现从睡眠时间在 与
与 个小时的学生中抽取2人,问能在这两个睡眠时间内各抽到1个学生的概率是多少?
个小时的学生中抽取2人,问能在这两个睡眠时间内各抽到1个学生的概率是多少?
(本题满分14分)
某校高三的某次数学测试中,对其中100名学生的成绩进行分析,按成绩分组,得到的频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第1组 |
|
15 |
① |
|
第2组 |
|
② |
0.35 |
|
第3组 |
|
20 |
0.20 |
|
第4组 |
|
20 |
0.20 |
|
第5组 |
|
10 |
0.10 |
|
合计 |
|
100 |
1.00 |
(1)求出频率分布表中①、②位置相应的数据;
(2)为了选拔出最优秀的学生参加即将举行的数学竞赛,学校决定在成绩较高的第3、4、5组中分层抽样取5名学生,则第4、5组每组各抽取多少名学生?
(3)为了了解学生的学习情况,学校又在这5名学生当中随机抽取2名进行访谈,求第4组中至少有一名学生被抽到的概率是多少?

 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行、从左往右数第
行、从左往右数第 个数.
个数. ,求
,求 的值;
的值;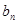 ,求证
,求证 .(本题满分14分)
.(本题满分14分) 层,总开发费用为
层,总开发费用为 万元,求函数
万元,求函数








