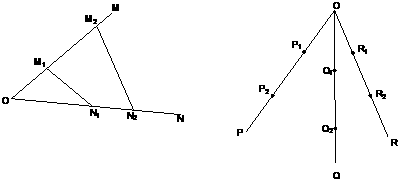
题目内容
设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点,若用f(n)表示这n条直线交点的个数,则f(4)= ______________;当n>4时,f(n)=______________.
思路解析:通过观察不难发现每增加一条直线,交点增加的个数等于原来直线的条数.
由f(2)=0,f(3)=2,f(4)=5,f(5)=9,…
可得每增加一条直线,交点增加的个数等于原来直线的条数.
∴f(3)-f(2)=2,f(4)-f(3)=3,f(5)-f(4)=4,…,f(n)-f(n-1)=n-1.
累加得f(n)=f(2)+2+3+4+…+n-1=![]() (n+1)(n-2).
(n+1)(n-2).
答案:5 ![]() (n+1)(n-2)
(n+1)(n-2)
深化升华 本小题主要考查观察、分析、归纳推理、累加求通项公式等知识,是一个很灵活的题目,在解题的过程中要善于观察发现规律,通过规律来解决问题揭示本质.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目