题目内容
设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,f(n)=( )
分析:首先由图可得f(4)的值,进而逐一给出f(3),f(4),…,的值,分析可得从n-1条直线增加为n条直线时,交点的数目会增加n-1,即f(n)=f(n-1)+n-1,然后利用数列求和的办法计算可得答案.
解答: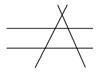 解:如图,4条直线有5个交点,故f(4)=5,
解:如图,4条直线有5个交点,故f(4)=5,
由f(3)=2,
f(4)=f(3)+3
…
分析可得,从n-1条直线增加为n条直线时,交点的数目会增加n-1,
f(n)=f(n-1)+n-1,
累加可得f(n)=2+3+…+(n-2)+(n-1)=
=
.
故选A.
 解:如图,4条直线有5个交点,故f(4)=5,
解:如图,4条直线有5个交点,故f(4)=5,由f(3)=2,
f(4)=f(3)+3
…
分析可得,从n-1条直线增加为n条直线时,交点的数目会增加n-1,
f(n)=f(n-1)+n-1,
累加可得f(n)=2+3+…+(n-2)+(n-1)=
| (n-2)(n-1+2) |
| 2 |
| (n-2)(n+1) |
| 2 |
故选A.
点评:本题考查的知识点是归纳推理与数列求和,根据f(3),f(4),…,f(n-1),f(n)然后分析项与项之间的关系,找出项与项之间的变化趋势是解决问题的关键.

练习册系列答案
 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目