题目内容
已知正弦函数y=sinx具有如下性质：若x1，x2，…xn∈（0，π），则
≤sin（
）（其中当 x1=x2=…=xn时等号成立）．根据上述结论可知，在△ABC中，sinA+sinB+sinC的最大值为
．
| sinx1+sinx2+…+sinxn |
| n |
| x1+x2+…+xn |
| n |
3
| ||
| 2 |
3
| ||
| 2 |
分析：利用正弦函数的性质可得：
≤sin
，变形得 sinA+sinB+sinC≤3sin
利用特殊三角函数值求得问题答案．
| sinA+sinB+sinC |
| 3 |
| A+B+C |
| 3 |
| π |
| 3 |
解答：解：∵已知正弦函数y=sinx具有如下性质：若x1，x2，…xn∈（0，π），则
≤sin（
），
且A、B、C∈（0，π），
∴
≤sin
，
即sinA+sinB+sinC≤3sin
=
，
所以sinA+sinB+sinC的最大值为
．
故答案为：
| sinx1+sinx2+…+sinxn |
| n |
| x1+x2+…+xn |
| n |
且A、B、C∈（0，π），
∴
| sinA+sinB+sinC |
| 3 |
| A+B+C |
| 3 |
即sinA+sinB+sinC≤3sin
| π |
| 3 |
3
| ||
| 2 |
所以sinA+sinB+sinC的最大值为
3
| ||
| 2 |
故答案为：
3
| ||
| 2 |
点评：本题主要考查三角函数的最值问题．考查了考生运用所给条件分析问题的能力和创造性解决问题的能力．
练习册系列答案
相关题目
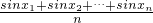≤sin（
）（其中当 x1=x2=…=xn时等号成立）．根据上述结论可知，在△ABC中，sinA+sinB+sinC的最大值为________．
≤sin（
）（其中当 x1=x2=…=xn时等号成立）．根据上述结论可知，在△ABC中，sinA+sinB+sinC的最大值为 ．
≤sin（
）（其中当 x1=x2=…=xn时等号成立）．根据上述结论可知，在△ABC中，sinA+sinB+sinC的最大值为 ．
≤sin（
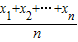）（其中当 x1=x2=…=xn时等号成立）．根据上述结论可知，在△ABC中，sinA+sinB+sinC的最大值为 ．