题目内容
已知双曲线的方程为
-
=1(a>0,b>0),过左焦点F1作斜率为
的直线交双曲线的右支于点P,且y轴平分线段F1P,则双曲线的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、2+
|
分析:首先写出直线l的方程y=
(x-c),然后求出线段F1P的中点坐标,进而得到p点坐标并代入双曲线方程,结合c2=a2+b2求出c2=3a2,即可得到结果.
| ||
| 3 |
解答:解:过焦点F1(-c,0)的直线L的方程为:y=
(x-c),
直线L交双曲线右支于点P,且y轴平分线F1P,
则交y轴于点Q(0,
c).
设点P的坐标为(x,y),
∴x+c=2c,y=
P点坐标(c,
),
代入双曲线方程得:
-
=
,
又∵c2=a2+b2,
∴c2=3a2,
∴e=
故选C.
| ||
| 3 |
直线L交双曲线右支于点P,且y轴平分线F1P,
则交y轴于点Q(0,
| ||
| 3 |
设点P的坐标为(x,y),
∴x+c=2c,y=
2
| ||
| 3 |
P点坐标(c,
2
| ||
| 3 |
代入双曲线方程得:
| 1 |
| a2 |
| 4 |
| 3b2 |
| 1 |
| c2 |
又∵c2=a2+b2,
∴c2=3a2,
∴e=
| 3 |
故选C.
点评:本题考查了双曲线的性质以及与直线的关系,关键是用含有c的式子表示出p的坐标,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
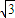 y=0和x+
y=0和x+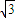 y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )
y=0,双曲线上的点满足不等式x2-3y2<0,已知双曲线的焦距为4,则双曲线的准线方程为( )