题目内容
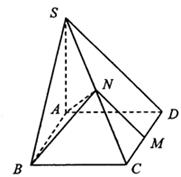
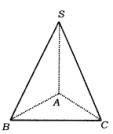
如图所示,已知SA、SB、SC是由一点S引出的不共面的三条射线,∠ASC=∠ASB=45°,∠BSC=60°,∠SAB=90°,求证:AB⊥SC.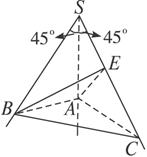
证明:设SA=a,并过A作AE⊥SC于E,
则从∠ASC=45°,知SE=AE=SA·sin45°=![]() a,
a,
连结BE,
因在Rt△SAB中,∠BAS=90°,
故SB=![]() ,AB=SA=a.
,AB=SA=a.
在△SBE中,又知∠BSE=60°,运用余弦定理得
BE2=SE2+SB2-2SE·SBcos60°=(![]() a)2+(
a)2+(![]() a)2-2·
a)2-2·![]() a·
a·![]() a·
a·![]() =
=![]() a2,
a2,
即BE=![]() a.
a.
在△BAE中,
因AB2+AE2=a2+(![]() a)2=
a)2=![]() a2=BE2,
a2=BE2,
由勾股定理逆定理,知∠BAE=90°,
即AB⊥AE,
又SA∩AE=A,于是AB⊥平面SAC.
又SC![]() 平面SAC,知AB⊥SC.
平面SAC,知AB⊥SC.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
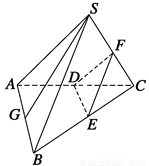
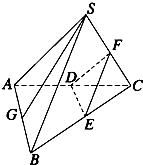 如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.
如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC,SG为△SAB上的高,D、E、F分别是AC、BC、SC的中点,试判断SG与平面DEF的位置关系,并给予证明.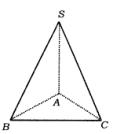
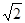 .
.