题目内容
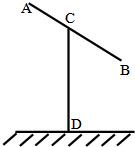某建筑工地上所用的金属支架由AB与CD组成，如图所示，根据要求，AB至少长2a（a＞2）m，C为AB中点，B到D的距离比CD的长小1m．∠BCD=60°．已知金属支架的材料每米的价格为10元．（1）设AB=2x，CD=y，试用x表示y；
（2）怎样设计AB、CD的长，可使建造这个支架的成本最低？
分析：（1）△BCD中，BC=x，CD=y，∠BCD=60°，由余弦定理可求BD；又BD比CD小1，可得x，y的关系式；
（2）由造价函数：W=10（2x+y）=10（2x+
）（其中x≥a＞2），不妨设t=x-2≥a-2＞0，化简W为t的函数容易求出结果；
（2）由造价函数：W=10（2x+y）=10（2x+
| x2-1 |
| x-2 |
解答：解：（1）如图，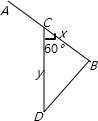
由余弦定理得：BD2=x2+y2-2xycos60°，∴BD=
；
由题意知，BD=CD-1，即
=y-1，∴y=
（其中x≥a＞2）；
（2）设支架的造价为：W=10（2x+y），不妨令z=2x+y=2x+
，
如果设t=x-2，那么t≥a-2＞0，∴z=2（t+2）+
=3（t+
）+8；
当a-2＞1，即a＞3时，∵z=3(t+
)+8在[a-2，+∞）上单调递增，∴x=a时，有AB=2a，CD=
，这时造价W的值最小；
当 2＜a≤3时，t=1，x=3，这时造价W的值也最小，且有AB=6，CD=8．
由余弦定理得：BD2=x2+y2-2xycos60°，∴BD=| x2+y2-xy |
由题意知，BD=CD-1，即
| x2+y2 -xy |
| x2-1 |
| x-2 |
（2）设支架的造价为：W=10（2x+y），不妨令z=2x+y=2x+
| x2-1 |
| x-2 |
如果设t=x-2，那么t≥a-2＞0，∴z=2（t+2）+
| (t+2)2-1 |
| t |
| 1 |
| t |
当a-2＞1，即a＞3时，∵z=3(t+
| 1 |
| t |
| a2-1 |
| a-2 |
当 2＜a≤3时，t=1，x=3，这时造价W的值也最小，且有AB=6，CD=8．
点评：本题借助三角形的余弦定理建立函数解析式，考查函数的最值问题，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
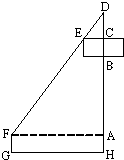如图，在某建筑工地上有一个吊臂长DF=24m的吊车，吊车底座FG高1．m．现准备把一个底半径为3m、高2m的圆柱形工件吊起平放到15m高的桥墩上．（注：当物件与吊臂接触后，钢索CD长可通过顶点D处的滑轮自动调节并保持物件始终与吊臂接触，且与工件的中心在一条垂直线上．）
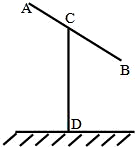某建筑工地上所用的金属支架由AB与CD组成，如图所示，根据要求，AB至少长2a（a＞2）m，C为AB中点，B到D的距离比CD的长小1m．∠BCD=60°．已知金属支架的材料每米的价格为10元．两种大小不同的钢板可按下表截成A,B,C三种规格成品:
|
| A规格 | B规格 | C规格 |
| 第一种钢板 | 2 | 1 | 1 |
| 第二种钢板 | 1 | 2 | 3 |
某建筑工地需A，B，C三种规格的成品分别为15，18，27块，问怎样截这两种钢板，可得所需三种规格成品，且所用钢板张数最小.