题目内容
一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是
．
分析：如图所示，直线a∥α，a∥β，α∩β=b，求证a∥b．只需考虑线面平行的性质定理及平行公理即可．
解答：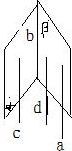
解：由a∥α得，经过a的平面与α相交于直线c，
则a∥c，
同理，设经过a的平面与β相交于直线d，
则a∥d，由平行公理得：c∥d，
则c∥β，又c?α，α∩β=b，所以c∥b，
又a∥c，所以a∥b．
故答案为：平行．
解：由a∥α得，经过a的平面与α相交于直线c，则a∥c，
同理，设经过a的平面与β相交于直线d，
则a∥d，由平行公理得：c∥d，
则c∥β，又c?α，α∩β=b，所以c∥b，
又a∥c，所以a∥b．
故答案为：平行．
点评：本题考查线面平行的判定与性质定理及平行公理，要注意线面平行的判定与性质的综合应用．
练习册系列答案
相关题目