题目内容
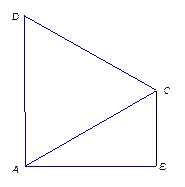
如图1,在直角梯形 中,
中, ,
, ,
,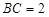 ,
,
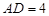 . 把
. 把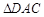 沿对角线
沿对角线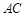 折起到
折起到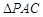 的位置,如图2所示,使得点
的位置,如图2所示,使得点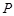 在平面
在平面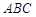 上的正投影
上的正投影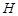 恰好落在线段
恰好落在线段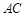 上,连接
上,连接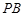 ,点
,点 分别为线段
分别为线段 的中点.
的中点.
(I)求证:平面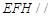 平面
平面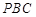 ;
;
(II)求直线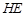 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(III)在棱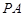 上是否存在一点
上是否存在一点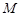 ,使得
,使得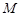 到点
到点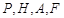 四点的距离相等?请说明理由.
四点的距离相等?请说明理由.

(I) 详见解析; (II) ;
(III) 存在点M满足条件.
;
(III) 存在点M满足条件.
【解析】
试题分析:(I)借助三角形中位线得到线线平行,进而得到面面平行;(II)建立空间直角坐标系,应用空间向量知识求线面角;(III) 记点 为
为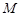 ,证明即可.
,证明即可.
试题解析:
(I)因为点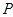 在平面
在平面 上的正投影
上的正投影 恰好落在线段
恰好落在线段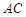 上
上
所以 平面
平面 ,所以
,所以
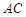 1分
1分
因为在直角梯形 中,
中,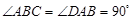 ,
,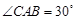 ,
,
 ,
,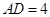
所以 ,
, ,所以
,所以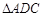 是等边三角形,
是等边三角形,
所以 是
是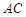 中点, 2分
中点, 2分
所以 3分
3分
同理可证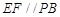
又
所以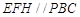 平面
平面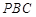 5分
5分
(II)在平面 内过
内过 作
作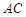 的垂线
的垂线
如图建立空间直角坐标系,

则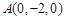 ,
, ,
,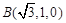 6分
6分
因为 ,
,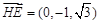
设平面 的法向量为
的法向量为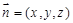
因为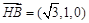 ,
,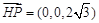
所以有 ,即
,即 ,
,
令 则
则 所以
所以  8分
8分
 10分
10分
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为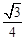 11分
11分
(III)存在,事实上记点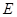 为
为 即可
12分
即可
12分
因为在直角三角形 中,
中,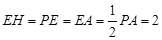 ,
13分
,
13分
在直角三角形 中,点
中,点

所以点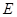 到四个点
到四个点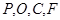 的距离相等
14分
的距离相等
14分
考点:1、面面平行的判定定理;2、直线与平面所成的角;3、立体几何中的探索性问题.

 名校通行证有效作业系列答案
名校通行证有效作业系列答案 中,
中,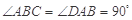 ,
,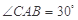 ,
,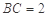 ,
,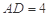 . 把
. 把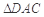 沿对角线
沿对角线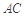 折起到
折起到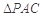 的位置,如图2所示,使得点
的位置,如图2所示,使得点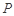 在平面
在平面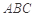 上的正投影
上的正投影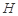 恰好落在线段
恰好落在线段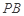 ,点
,点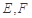 分别为线段
分别为线段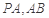 的中点.
的中点. 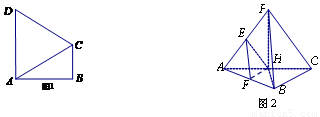
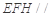 平面
平面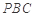 ;
;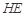 与平面
与平面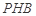 所成角的正弦值;
所成角的正弦值;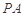 上是否存在一点
上是否存在一点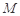 ,使得
,使得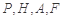 四点的距离相等?请说明理由.
四点的距离相等?请说明理由. 中,
中,  ,
,  ,
, ,
, 为线段
为线段 的中点. 将
的中点. 将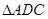 沿
沿 折起,使平面
折起,使平面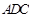
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示. 平面
平面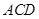 ;
;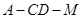 的余弦值.
的余弦值. 
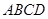 中,
中,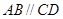 ,
, ,且
,且 .
.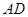 为一边向形外作正方形
为一边向形外作正方形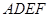 ,然后沿边
,然后沿边 为
为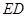 的中点,如图2.
的中点,如图2.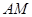 ∥平面
∥平面 ;
;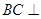 平面
平面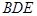 ;
;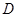 到平面
到平面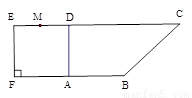

 图
图
 中,
中,  ,
,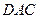 沿对角线
沿对角线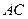 折起后如图2所示(点
折起后如图2所示(点 记为点
记为点 ), 点
), 点 上的正投影
上的正投影 落在线段
落在线段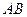 上, 连接
上, 连接 .
. 与平面
与平面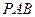 所成的角的大小;
所成的角的大小; 的大小的余弦值.
的大小的余弦值.