题目内容
已知函数![]() 其中
其中![]() 为常数,函数
为常数,函数![]() 在其图像和与坐标轴的交点处的切线为
在其图像和与坐标轴的交点处的切线为![]() ,函数
,函数![]() 在其图像与坐标轴的交点处的切线为
在其图像与坐标轴的交点处的切线为![]() ,
,![]() 平行于
平行于![]() 。
。
(1)求函数![]() 的解析式;
的解析式;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
(1)![]() ,
,![]() 的图像与坐标轴的交点为
的图像与坐标轴的交点为![]() ,
,
![]() 的图像与坐标轴的交点为
的图像与坐标轴的交点为![]() ,由题意得
,由题意得![]()
即![]() , 又
, 又![]()
![]()
(2)由题意![]() ,当
,当![]() 时,
时,![]()
令![]() ,
,![]()
令![]()
![]() ,
,
当![]() 时,
时,![]() 单调递增。
单调递增。
![]() ,由
,由![]() 在
在![]() 上恒成立, 得
上恒成立, 得![]()
当![]() 时,
时,![]() ,可得
,可得![]()
![]() 单调递增。由
单调递增。由![]() 在
在![]() 上恒成立,得
上恒成立,得![]()
综上,可知![]() 。
。

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (
( 为常数,
为常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与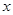 轴平行.
轴平行. 的单调区间;
的单调区间; ,其中
,其中 为
为 .
.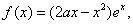 其中
其中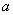 为常数,且
为常数,且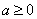 。
。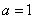 时,求函数
时,求函数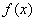 的极值点;
的极值点;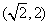 内单调递减,求
内单调递减,求