题目内容
已知函数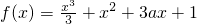 ,动直线l的斜率k=2.
,动直线l的斜率k=2.
(1)若存在直线l与f(x)的图象相切,求a的取值范围;
(2)若恰好有一条直线l与f(x)的图象相切,求直线l的方程;
(3)若动直线l与f(x)的图象相切点A(x1,y1),且x1∈[-2,2],求a的取值范围.
解:由题意得f'(x)=x2+2x+3a.
(1)若存在直线l与f(x)的图象相切,设l的斜率为k,
则x2+2x+3a=2,3a=2-x2-2x≤3?a≤1,
∴a的取值范围(-∞,1];
(2)若恰好有一条直线l与f(x)的图象相切,
设切点M(x,y),则x2+2x+3a=2有惟一解,?△=0?a=1,
且x=-1,切点M(-1,- ),
),
∴直线l的方程为:y+ =2(x+1),即:2x+y+
=2(x+1),即:2x+y+ =0;
=0;
(3)若动直线l与f(x)的图象相切点A(x1,y1),
则x12+2x1+3a=2且x1∈[-2,2],
3a=2-x12-2x1∈[-6,3],?a∈[-2,1]
故a的取值范围[-2,1].
分析:(1)求得f'(x)=x2+2x+3a.根据已知条件可得f′(x)=2,利用二次函数的性质可以得出a的取值范围;
(2)若恰好有一条直线l与f(x)的图象相切,设切点M(x,y),则x2+2x+3a=2有惟一解,结合根的判别式求出x及切点,最后写出直线l的方程;
(3)若动直线l与f(x)的图象相切点A(x1,y1),则x12+2x1+3a=2且x1∈[-2,2],3a=2-x12-2x1∈[-6,3],求出函数2-x12-2x1在区间[-2,2]上的值域,实数3a也应在这个值域中,因此可以得到实数a的取值范围.
点评:本题主要考查了利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力与转化思想.属于基础题.
(1)若存在直线l与f(x)的图象相切,设l的斜率为k,
则x2+2x+3a=2,3a=2-x2-2x≤3?a≤1,
∴a的取值范围(-∞,1];
(2)若恰好有一条直线l与f(x)的图象相切,
设切点M(x,y),则x2+2x+3a=2有惟一解,?△=0?a=1,
且x=-1,切点M(-1,-
 ),
),∴直线l的方程为:y+
 =2(x+1),即:2x+y+
=2(x+1),即:2x+y+ =0;
=0;(3)若动直线l与f(x)的图象相切点A(x1,y1),
则x12+2x1+3a=2且x1∈[-2,2],
3a=2-x12-2x1∈[-6,3],?a∈[-2,1]
故a的取值范围[-2,1].
分析:(1)求得f'(x)=x2+2x+3a.根据已知条件可得f′(x)=2,利用二次函数的性质可以得出a的取值范围;
(2)若恰好有一条直线l与f(x)的图象相切,设切点M(x,y),则x2+2x+3a=2有惟一解,结合根的判别式求出x及切点,最后写出直线l的方程;
(3)若动直线l与f(x)的图象相切点A(x1,y1),则x12+2x1+3a=2且x1∈[-2,2],3a=2-x12-2x1∈[-6,3],求出函数2-x12-2x1在区间[-2,2]上的值域,实数3a也应在这个值域中,因此可以得到实数a的取值范围.
点评:本题主要考查了利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力与转化思想.属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
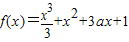 ,动直线l的斜率k=2.
,动直线l的斜率k=2.