题目内容
已知函数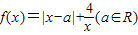 .
.(1)若a=0,求不等式f(x)≥0的解集;
(2)若对于一切x∈(0,+∞),不等式f(x)≥1恒成立,求a的取值范围.
【答案】分析:(1)将a=0代入,根据绝对值的意义,分别讨论x>0和x<0时,不等式的解集情况,最后综合讨论结果,可得答案;
(2)利用零点分段法,可将函数解析式化为f(x)=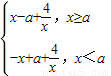 ,分当a≤0时,当a∈(0,2)时和当a≥2时,三种情况分别讨论不等式f(x)≥1恒成立时,a的取值范围,最后综合讨论结果,可得答案.
,分当a≤0时,当a∈(0,2)时和当a≥2时,三种情况分别讨论不等式f(x)≥1恒成立时,a的取值范围,最后综合讨论结果,可得答案.
解答:解:(1)当a=0时,函数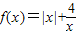
不等式f(x)≥0可化为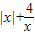 ≥0
≥0
当x>0时,不等式恒成立;
当x<0时,不等式可化为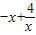 ≥0
≥0
解得x≤-2
综上不等式的解集为(-∞,-2]∪(0,+∞). …(3分)
(2)f(x)=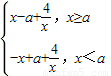 …(5分)
…(5分)
①当a≤0时,f(x)=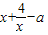 ≥4-a≥1,
≥4-a≥1,
∴a≤3.又a≤0,
所以,a≤0满足题意. …(7分)
②当a∈(0,2)时,函数f(x)的在(0,2)上单调递减,在(2,+∞)上单调递增,
所以f(x)=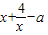 ≥4-a≥1,
≥4-a≥1,
∴a≤3.
又因为a∈(0,2),
所以,a∈(0,2)满足题意. (10分)
③当a≥2时,函数f(x)的在(0,a)上单调递减,在(a,+∞)上单调递增,
所以f(x)min=f(a)=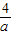 ≥1,
≥1,
∴a≤4,
又因为a>2,
所以a∈[2,4]满足题意. (13分)
综上,a的取值范围是(-∞,4].…(14分)
点评:本题以函数恒成立为载体考查了绝对值函数问题的解答方法,遇到绝对值问题时,关键在于去掉绝对值符号,分类讨论是解答时常用的方法.
(2)利用零点分段法,可将函数解析式化为f(x)=
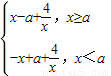 ,分当a≤0时,当a∈(0,2)时和当a≥2时,三种情况分别讨论不等式f(x)≥1恒成立时,a的取值范围,最后综合讨论结果,可得答案.
,分当a≤0时,当a∈(0,2)时和当a≥2时,三种情况分别讨论不等式f(x)≥1恒成立时,a的取值范围,最后综合讨论结果,可得答案.解答:解:(1)当a=0时,函数
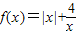
不等式f(x)≥0可化为
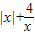 ≥0
≥0当x>0时,不等式恒成立;
当x<0时,不等式可化为
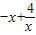 ≥0
≥0解得x≤-2
综上不等式的解集为(-∞,-2]∪(0,+∞). …(3分)
(2)f(x)=
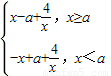 …(5分)
…(5分)①当a≤0时,f(x)=
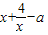 ≥4-a≥1,
≥4-a≥1,∴a≤3.又a≤0,
所以,a≤0满足题意. …(7分)
②当a∈(0,2)时,函数f(x)的在(0,2)上单调递减,在(2,+∞)上单调递增,
所以f(x)=
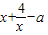 ≥4-a≥1,
≥4-a≥1,∴a≤3.
又因为a∈(0,2),
所以,a∈(0,2)满足题意. (10分)
③当a≥2时,函数f(x)的在(0,a)上单调递减,在(a,+∞)上单调递增,
所以f(x)min=f(a)=
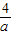 ≥1,
≥1,∴a≤4,
又因为a>2,
所以a∈[2,4]满足题意. (13分)
综上,a的取值范围是(-∞,4].…(14分)
点评:本题以函数恒成立为载体考查了绝对值函数问题的解答方法,遇到绝对值问题时,关键在于去掉绝对值符号,分类讨论是解答时常用的方法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
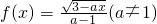 .
.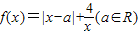 .
.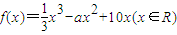 .
.