题目内容
(文科)若实数a,b满足|a-b|≥1,则a2+b2( )A.最小值为

B.最大值为

C.最大值为
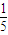
D.最小值为
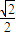
【答案】分析:实数a,b满足|a-b|≥1,确定其区域,明确a2+b2的几何意义,根据图形,即可求得结论.
解答:解:实数a,b满足|a-b|≥1,即a≥1+b或a≤-1+b,满足的区域如图,为两条平行线外的部分
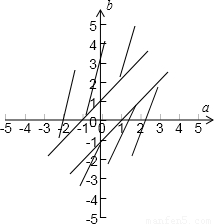
a2+b2的几何意义是区域内的点到原点的距离的平方,根据图形可知a2+b2的最小值为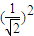 =
=
故选A.
点评:本题考查线性规划知识的运用,解题的关键是确定平面区域,明确目标函数的几何意义,属于中档题.
解答:解:实数a,b满足|a-b|≥1,即a≥1+b或a≤-1+b,满足的区域如图,为两条平行线外的部分

a2+b2的几何意义是区域内的点到原点的距离的平方,根据图形可知a2+b2的最小值为
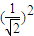 =
=
故选A.
点评:本题考查线性规划知识的运用,解题的关键是确定平面区域,明确目标函数的几何意义,属于中档题.

练习册系列答案
相关题目



