题目内容
曲线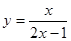
在点（1,1）处的切线方程为____________________.
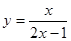在点（1,1）处的切线方程为____________________.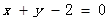
解：设切线的斜率为k，则切线的方程为y=kx-k+1，
y=kx-k+1
y="x" /（2x-1） 转化为2kx2-（3k-1）x+k-1=0，
讨论：当k=0时，验证不符合题意；所以k≠0，所以2kx2-（3k-1）x+k-1=0为一元二次方程．
令△=（3k-1）2-8k（k-1）=0，得到k=-1，即切线方程为x+y-2=0
故答案为x+y-2=0．
y=kx-k+1
y="x" /（2x-1） 转化为2kx2-（3k-1）x+k-1=0，
讨论：当k=0时，验证不符合题意；所以k≠0，所以2kx2-（3k-1）x+k-1=0为一元二次方程．
令△=（3k-1）2-8k（k-1）=0，得到k=-1，即切线方程为x+y-2=0
故答案为x+y-2=0．
练习册系列答案
阳光同学一线名师全优好卷系列答案
相关题目
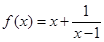，曲线
过点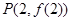
处的切线与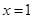直线
和直线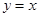
所围三角形的面积为_________。
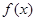的导数为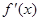
，下列说法正确的有________.
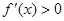的解集为函数的增区间.
.
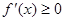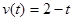，质点作直线运动，则此质点体在
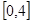时间内的路程为 （ ）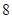
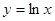在点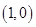
处的切线方程为________． 
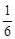处的切线的倾斜角是
π
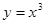在点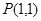
的切线方程为 ．
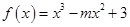，若
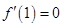，则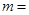
.
___________.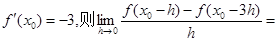