题目内容
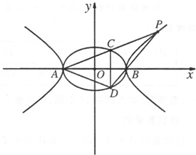 (2012•湛江二模)已知椭圆C1:
(2012•湛江二模)已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
(1)若a=2b,求椭圆C1及双曲线C2的离心率;
(2)若△ACD和△PCD的面积相等,求点P的坐标(用a,b表示).
分析:(1)根据a=2b,结合椭圆中,c2=a2-b2=
a2,双曲线中,c2=a2+b2=
a2,即可求得椭圆C1及双曲线C2的离心率;
(2)设P、C的坐标分别为(x0,y0),(x1,y1),根据△ACD和△PCD的面积相等,可得
=x1,
=y1,分别代入椭圆、双曲线方程,联立方程,即可求得点P的坐标.
| 3 |
| 4 |
| 5 |
| 4 |
(2)设P、C的坐标分别为(x0,y0),(x1,y1),根据△ACD和△PCD的面积相等,可得
| -a+x0 |
| 2 |
| 0+y0 |
| 2 |
解答:解:(1)∵a=2b,∴在椭圆C1:
+
=1(a>b>0)中,c2=a2-b2=
a2
∴椭圆C1的离心率为e1=
=
;
在双曲线C2中,c2=a2+b2=
a2,
∴双曲线C2的离心率为e2=
=
;
(2)设P、C的坐标分别为(x0,y0),(x1,y1)
由题意知A,B的坐标分别为(-a,0),(a,0)
∵△ACD和△PCD的面积相等,
∴|AC|=|PC|
∴
=x1,
=y1
代入椭圆C1:
+
=1得b2x02-2ab2x0+a2b2 +a2y02=4a2b2①
∵P(x0,y0)是双曲线C2:
-
=1右支x轴上方的一点,
∴a2y02=b2x02- a2b2②
②代入①化简可得x02- ax0 -2a2=0
∴x0=2a或-a(舍去)
∴y0=
=
b
∴点P的坐标为(2a,
b).
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
∴椭圆C1的离心率为e1=
| c |
| a |
| ||
| 2 |
在双曲线C2中,c2=a2+b2=
| 5 |
| 4 |
∴双曲线C2的离心率为e2=
| c |
| a |
| ||
| 2 |
(2)设P、C的坐标分别为(x0,y0),(x1,y1)
由题意知A,B的坐标分别为(-a,0),(a,0)
∵△ACD和△PCD的面积相等,
∴|AC|=|PC|
∴
| -a+x0 |
| 2 |
| 0+y0 |
| 2 |
代入椭圆C1:
| x2 |
| a2 |
| y2 |
| b2 |
∵P(x0,y0)是双曲线C2:
| x2 |
| a2 |
| y2 |
| b2 |
∴a2y02=b2x02- a2b2②
②代入①化简可得x02- ax0 -2a2=0
∴x0=2a或-a(舍去)
∴y0=
|
| 3 |
∴点P的坐标为(2a,
| 3 |
点评:本题考查椭圆与双曲线的标准方程与几何性质,考查学生的计算能力,解题的关键是利用△ACD和△PCD的面积相等,寻求坐标之间的关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
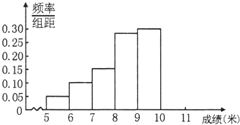 (2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6.
(2012•湛江二模)某市为了解今年高中毕业生的身体素质状况,从本市某校高中毕业班中抽取一个班进行实心球测试,成绩在8米及以上的为合格.把所得数据进行整理后,分成6组画出频率分布直方图的一部分(如图),已知第一小组为[5,6),从左到右前5个小组的频率分别为0.06,0.10,0.14,0.28,0.30.第6小组的频数是6. (2012•湛江二模)运行如图所示框图,坐标满足不等式组
(2012•湛江二模)运行如图所示框图,坐标满足不等式组 (2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=
(2012•湛江二模)如图,Rt△ABC中,∠C=90°,∠A=30°,圆O经过B、C且与AB、AC分别相交于D、E.若AE=EC=