题目内容
 已知函数f(x)=
已知函数f(x)=
|
(1)在下面给定的坐标系中作出函数f(x)的图象;
(2)写出函数f(x)的零点和值域;
(3)若关于x的方程f(x)=k有两个不同的实根,求实数k的取值范围.
分析:(1)由所给的函数的解析式,把它化为分段函数的形式,从而画出 f(x) 的图象.
(2)结合函数f(x)的图象,数形结合得出f(x)的零点和值域.
(3)由题意可得,函数f(x) 的图象和直线y=k有2个不同的交点,数形结合求得实数k的取值范围.
(2)结合函数f(x)的图象,数形结合得出f(x)的零点和值域.
(3)由题意可得,函数f(x) 的图象和直线y=k有2个不同的交点,数形结合求得实数k的取值范围.
解答:解:(1)由函数的解析式可得 f(x)=
,它的图象如图所示:
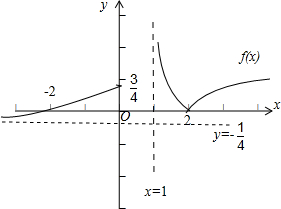
(2)由函数f(x)的图象可得函数的零点为 x=-2和 x=2,值域为(-
,+∞).
(3)若关于x的方程f(x)=k有两个不同的实根,则函数f(x) 的图象和直线y=k有2个不同的交点,
故k>
,故实数k的取值范围为(-
,+∞).
|

(2)由函数f(x)的图象可得函数的零点为 x=-2和 x=2,值域为(-
| 1 |
| 4 |
(3)若关于x的方程f(x)=k有两个不同的实根,则函数f(x) 的图象和直线y=k有2个不同的交点,
故k>
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题主要考查对数型复合函数的性质以及应用,函数的零点的定义,函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|