题目内容

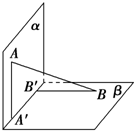精英家教网如图，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为
π
4
和
π
6
．过A、B分别作两平面交线的垂线，垂足为A′、B′，则AB：A′B′=（　　）
A、2：1B、3：1
C、3：2D、4：3
分析：设AB的长度为a用a表示出A'B'的长度，即可得到两线段的比值．
解答：解：连接AB'和A'B，设AB=a，可得AB与平面α所成的角为∠BAB′=
π
4
，
在Rt△BAB'中有AB'=
2
2
a，同理可得AB与平面β所成的角为∠ABA′=
π
6
，
所以A′A=
1
2
a，因此在Rt△AA'B'中A'B'=
(
2
2
a)2-(
1
2
a)2
=
1
2
a，
所以AB：A'B'=a：
1
2
a=2：1，
故选A．
点评：本题主要考查直线与平面所成的角以及线面的垂直关系，要用到勾股定理及直角三角形中的边角关系．有一定的难度
练习册系列答案
相关题目
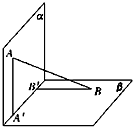精英家教网如图，已知等腰△ABC的底边BC=3，顶角为120°，D是BC边上一点，且BD=1．把△ADC沿AD折起，使得平面CAD⊥平面ABD，连接BC形成三棱锥C-ABD．
（Ⅰ） ①求证：AC⊥平面ABD；②求三棱锥C-ABD的体积；
（Ⅱ） 求AC与平面BCD所成的角的正弦值．
精英家教网如图，平面α⊥平面β，A∈α，B∈β，AB与平面α、β所成的角分别为
π
4
和
π
6
，过A、B分别作两平面交线的垂线，垂足为A′、B′，若AB=12，求A′B′的长度．
如图（1）直线l∥AB，且与CA，CB分别相交于点E，F，EF与AB间的距离是d，点P是线段EF上任意一点，Q是线段AB上任意一点，则|PQ|的最小值等于d．类比上述结论我们可以得到：在图（2）中，平面α∥平面ABC，且与DA，DB，DC分别相交于点E，F，G，平面α与平面ABC间的距离是m，
a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
a，b分别是平面α与平面ABC内的任意一条直线，则a，b间距离的最小值是m．
或P，Q分别是平面α与平面ABC内的任意一点，则P，Q间距离的最小值是m．
．
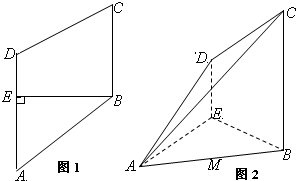（2013•威海二模）如图1，在梯形ABCD中，BC∥DA，BE⊥DA，EA=EB=BC=2，DE=1，将四边形DEBC沿BE折起，使平面DEBC垂直平面ABE，如图2，连结AD，AC．设M是AB上的动点．
（Ⅰ）若M为AB中点，求证：ME∥平面ADC；
（Ⅱ）若AM=
13
AB，求三棱锥M-ADC的体积．

（本小题满分12分）

如图，平面平面，点E、F、O分别为线段PA、PB、AC的中点，点G是线段CO的中点，

，．

求证:   （Ⅰ）平面；

（Ⅱ）∥平面．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网