题目内容
设△ABC的三内角A、B、C成等差数列,sinA 、sinB、 sinC成等比数列,则这个三角形的形状是( )
A.直角三角形 B. 钝角三角形
C.等腰直角三角形 D.等边三角形
A.直角三角形 B. 钝角三角形
C.等腰直角三角形 D.等边三角形
D
解:∵△ABC的三内角A、B、C成等差数列,
∴∠B=60°,∠A+∠C=120°①;
又sinA、sinB、sinC成等比数列,
∴sin2B=sinA•sinC=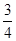 ,②由①②得:sinA•sin(120°-A)=sinA•(sin120°cosA-cos120°sinA)=
,②由①②得:sinA•sin(120°-A)=sinA•(sin120°cosA-cos120°sinA)=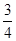 ,
,
∴sin(2A-30°)=1,又0°<∠A<120°∴∠A=60°.故选D
∴∠B=60°,∠A+∠C=120°①;
又sinA、sinB、sinC成等比数列,
∴sin2B=sinA•sinC=
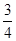 ,②由①②得:sinA•sin(120°-A)=sinA•(sin120°cosA-cos120°sinA)=
,②由①②得:sinA•sin(120°-A)=sinA•(sin120°cosA-cos120°sinA)=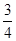 ,
,∴sin(2A-30°)=1,又0°<∠A<120°∴∠A=60°.故选D

练习册系列答案
相关题目
 满足递推公式
满足递推公式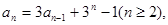 又
又 则使得
则使得 为等差数列的实数
为等差数列的实数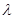 =
= 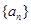 中,若
中,若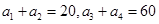 ,则
,则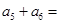 .
. 满足
满足  ,其中
,其中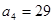 , 则这个数列的首项是( )
, 则这个数列的首项是( ) 满足
满足 ,且
,且 是
是 ,
, 的等差中项.
的等差中项.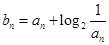 ,
, ,求使
,求使  成立的
成立的 的最小值.
的最小值.  的等差数列
的等差数列 的各项依次插入等比数列
的各项依次插入等比数列 中,将
中,将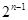 项的各组,得到数列
项的各组,得到数列 :b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若
:b1,a1,b2,b3,a2,b4,b5,b6,b7,a3,…,若 ,且
,且 ,则
,则 等于( )
等于( )
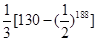
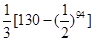

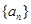 满足
满足 =
=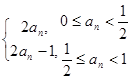 ,若
,若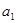 =
=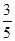 ,则
,则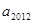 =____________
=____________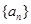 各项均为正数,且
各项均为正数,且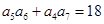 ,则
,则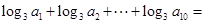
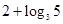
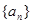 中,首项
中,首项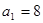 ,公比
,公比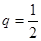 ,那么
,那么 的值是
的值是