题目内容
(12分) 在△ABC中,a、b、c分别为角A、B、C的对边,且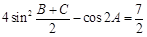 ,
,
(1)求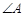 的度数;
的度数;
(2)若 ,
,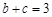 ,求b和c的值.
,求b和c的值.
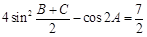 ,
,(1)求
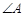 的度数;
的度数;(2)若
 ,
,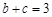 ,求b和c的值.
,求b和c的值. (1) A = 60°
(2)
(2)

本试题主要是考查了解三角形中边角的转化,以及余弦定理的运用。
(1)利用已知的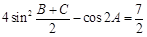 降幂倍角,然后得到关于角A的三角方程,得到结论。
降幂倍角,然后得到关于角A的三角方程,得到结论。
(2)由余弦定理可知a2 = b2 + c2-2bccosA = b2 + c2-bc =" (" b + c )2-3bc和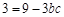 ,求解得到bc的值,然后结合
,求解得到bc的值,然后结合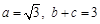 ,联立方程组得到结论。
,联立方程组得到结论。
解:(1)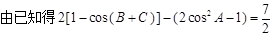 2分
2分
∵cos(B + C ) =-cosA,∴4cos2A-4cosA + 1 = 0 4分
∴(2cosA-1)2 = 0,即cosA =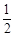
∴A = 60° 6分
(2) ∵a2 = b2 + c2-2bccosA = b2 + c2-bc =" (" b + c )2-3bc 9分
∵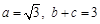
∴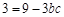 ,∴
,∴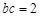 11分
11分
 12分
12分
(1)利用已知的
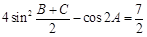 降幂倍角,然后得到关于角A的三角方程,得到结论。
降幂倍角,然后得到关于角A的三角方程,得到结论。(2)由余弦定理可知a2 = b2 + c2-2bccosA = b2 + c2-bc =" (" b + c )2-3bc和
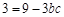 ,求解得到bc的值,然后结合
,求解得到bc的值,然后结合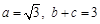 ,联立方程组得到结论。
,联立方程组得到结论。解:(1)
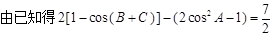 2分
2分∵cos(B + C ) =-cosA,∴4cos2A-4cosA + 1 = 0 4分
∴(2cosA-1)2 = 0,即cosA =
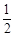
∴A = 60° 6分
(2) ∵a2 = b2 + c2-2bccosA = b2 + c2-bc =" (" b + c )2-3bc 9分
∵
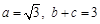
∴
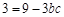 ,∴
,∴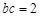 11分
11分 12分
12分
练习册系列答案
相关题目
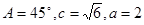 的△ABC的个数为m,则am的值为
的△ABC的个数为m,则am的值为  分别是角A,B,C的对边,
分别是角A,B,C的对边,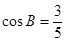 ,且
,且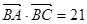 。
。 的值及△ABC的面积;
的值及△ABC的面积;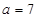 ,求角C的大小。
,求角C的大小。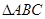 的三个内角满足
的三个内角满足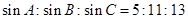 ,则
,则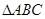 中,
中,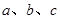 分别为角
分别为角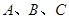 所对的三边,已知
所对的三边,已知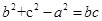 .
.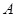 的值;
的值;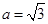 ,
,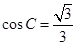 ,求
,求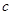 的长.
的长.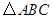 中,角
中,角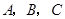 所对的边分别为
所对的边分别为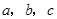 ,且
,且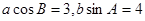 ,则
,则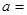 .
.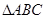 中,
中,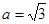 ,
,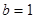 ,
, ,求角
,求角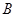 、边
、边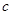 及
及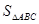 .
.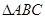 中,
中,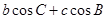 = .
= .