题目内容
已知两个数列3,7,11,…,139与2,9,16,…,142,则它们所有公共项的个数为( )
| A.4 | B.5 | C.6 | D.7 |
B
解析试题分析:由题意可知这两个数列分别是公差为4和7的等差数列,那么公共项组成公差为28(最小公倍数)的等差数列,记为数列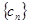 ,且
,且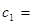 23,则
23,则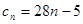 ,由
,由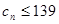 ,∴
,∴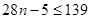 ,可得
,可得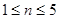 ,
,
所以选B.
考点:等差数列.

练习册系列答案
相关题目
等差数列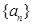 中,若
中,若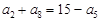 ,则
,则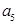 等于( )
等于( )
| A.3 | B.4 | C.5 | D.6 |
已知各项为正数的等差数列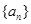 的前
的前 项和为
项和为 ,那么
,那么 的最大值为( )
的最大值为( )
| A.25 | B.50 | C.75 | D.100 |
已知等差数列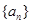 的前
的前 项和为
项和为 ,若
,若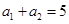 ,
,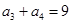 ,则
,则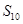 为( )
为( )
A.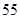 | B.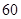 | C.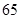 | D.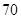 |
设等差数列{an}的前n项和为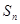 ,若
,若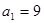 ,
,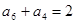 , 则当
, 则当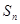 取最大值
取最大值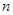 等于( )
等于( )
| A.4 | B.5 | C.6 | D.7 |
已知数列
 为等差数列,且
为等差数列,且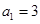 ,
, ,
,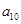 的值为( )
的值为( )
A.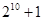 | B.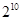 | C.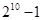 | D.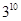 |
若等差数列 的公差
的公差 ,且
,且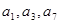 成等比数列,则
成等比数列,则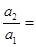 ( )
( )
| A.2 | B.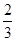 | C.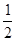 | D.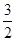 |
若三位数 被7整除,且
被7整除,且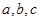 成公差非零的等差数列,则这样的整数共有( )个。
成公差非零的等差数列,则这样的整数共有( )个。
| A.4 | B.6 | C.7 | D.8 |
设等差数列{an}的前n项和为Sn,Sm-1=-2,Sm=0,Sm+1=3,则m= ( )
| A.3 | B.4 | C.5 | D.6 |