��Ŀ����
��֪ij��˾����ijƷ�Ʒ�װ����̶��ɱ�Ϊ10��Ԫ��ÿ����ǧ������Ͷ��2.7��Ԫ����ù�˾���ڹ�������Ʒ�Ʒ�װxǧ����ȫ�������꣬ÿǧ������������ΪR��x����Ԫ����R��x�����㣺��1����0��x��10ʱ����������������װ��ƽ����һ�ι�ϵ��x=3ǧ��ʱ��������Ϊ10.5��Ԫ��x=9ǧ��ʱ��������Ϊ8.1��Ԫ����2����x��10ʱ����������������װ�Ĺ�ϵʽΪ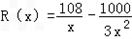 ��
��
��1��д��������W����Ԫ���������Ʒx��ǧ�����ĺ�������ʽ��
��2�������Ϊ����ǧ��ʱ���ù�ʽ����һƷ�Ʒ�װ���������������������
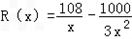 ��
����1��д��������W����Ԫ���������Ʒx��ǧ�����ĺ�������ʽ��
��2�������Ϊ����ǧ��ʱ���ù�ʽ����һƷ�Ʒ�װ���������������������
�⣺��1���ߵ�0��x��10ʱ����������������װ��ƽ����һ�ι�ϵ
�����R��x��=kx2+b
��x=3ǧ��ʱ��������Ϊ10.5��Ԫ��x=9ǧ��ʱ��������Ϊ8.1��Ԫ
��
��b=10.8��
�൱0��x��10ʱ������������������װ�Ĺ�ϵʽΪ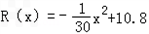
��0��x��10ʱ��W=xR��x������10+2.7x��=8.1x��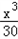 ��10��
��10��
��x��10ʱ��W=xR��x������10+2.7x��=98��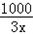 ��2.7x��
��2.7x��
��W=
��2���ٵ�0��x��10ʱ����W'=8.1��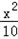 =0����x=9��
=0����x=9��
�ҵ�x�ʣ�0��9��ʱ��W'��0��
��x�ʣ�9��10��ʱ��W'��0��
�൱x=9ʱ��Wȡ���ֵ����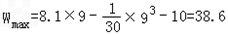
�ڵ�x��10ʱ��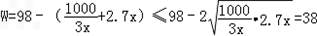
���ҽ���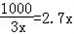 ����x=
����x=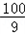 ʱ��W=38��
ʱ��W=38��
�ʵ�x=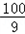 ʱ��Wȡ���ֵ38��
ʱ��Wȡ���ֵ38��
�ۺϢ٢�֪��x=9ʱ��Wȡ���ֵ38.6��Ԫ��
�ʵ������Ϊ9ǧ��ʱ���ù�˾����һƷ�Ʒ�װ���������������������
�����R��x��=kx2+b
��x=3ǧ��ʱ��������Ϊ10.5��Ԫ��x=9ǧ��ʱ��������Ϊ8.1��Ԫ
��

��b=10.8��

�൱0��x��10ʱ������������������װ�Ĺ�ϵʽΪ
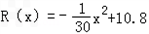
��0��x��10ʱ��W=xR��x������10+2.7x��=8.1x��
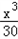 ��10��
��10����x��10ʱ��W=xR��x������10+2.7x��=98��
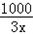 ��2.7x��
��2.7x����W=

��2���ٵ�0��x��10ʱ����W'=8.1��
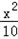 =0����x=9��
=0����x=9���ҵ�x�ʣ�0��9��ʱ��W'��0��
��x�ʣ�9��10��ʱ��W'��0��
�൱x=9ʱ��Wȡ���ֵ����
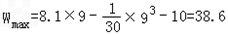
�ڵ�x��10ʱ��
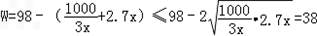
���ҽ���
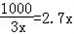 ����x=
����x=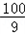 ʱ��W=38��
ʱ��W=38���ʵ�x=
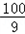 ʱ��Wȡ���ֵ38��
ʱ��Wȡ���ֵ38���ۺϢ٢�֪��x=9ʱ��Wȡ���ֵ38.6��Ԫ��
�ʵ������Ϊ9ǧ��ʱ���ù�˾����һƷ�Ʒ�װ���������������������

��ϰ��ϵ�д�
 �ο�����������100��ϵ�д�
�ο�����������100��ϵ�д� �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
�����Ŀ
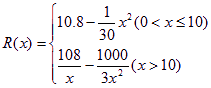 ��
�� ��Ԫ����
��Ԫ����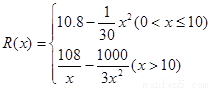 ��
�� ����Ԫ���������Ʒ��ǧ�����ĺ�������ʽ��
����Ԫ���������Ʒ��ǧ�����ĺ�������ʽ��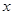 ǧ����ȫ�������꣬ÿǧ������������Ϊ
ǧ����ȫ�������꣬ÿǧ������������Ϊ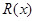 ��Ԫ����
��Ԫ����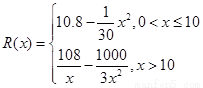 .
.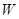 ����Ԫ�����������
����Ԫ�����������