题目内容
已知α+β=
，则（1+tanα）（1+tanβ）的值是（ ）
| π |
| 4 |
| A、-1 | B、1 | C、2 | D、4 |
分析：由α+β=
，得到tan（α+β）=1，利用两角和的正切函数公式化简tan（α+β）=1，即可得到所求式子的值．
| π |
| 4 |
解答：解：由α+β=
，得到tan（α+β）=tan
=1，
所以tan（α+β）=
=1，即tanα+tanβ=1-tanαtanβ，
则（1+tanα）（1+tanβ）=1+tanα+tanβ+tanαtanβ=2．
故选C
| π |
| 4 |
| π |
| 4 |
所以tan（α+β）=
| tanα+tanβ |
| 1-tanαtanβ |
则（1+tanα）（1+tanβ）=1+tanα+tanβ+tanαtanβ=2．
故选C
点评：此题考查学生灵活运用两角和与差的正切函数公式及特殊角的三角函数值化简求值，是一道基础题．
练习册系列答案
高效智能课时作业系列答案
相关题目
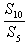=4+
，则cot(
+α)等于( )
B.4-
C.
D.
=4，则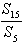
=（ ）。