题目内容
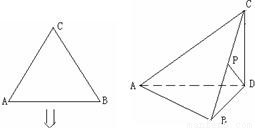
把边长为2的正三角形ABC沿BC上的高AD折成直二面角,设折叠后BC的中点为P,(I)求异面直线AC,PD所成的角的余弦值;
(II)求二面角C-AB-D的大小.
【答案】分析:(Ⅰ)以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系,求出向量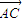 和
和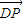 的坐标,利用向量的夹角公式即可求出所成角;
的坐标,利用向量的夹角公式即可求出所成角;
(Ⅱ)要求二面角C-AB-D的大小,即分别求出两平面的法向量,然后利用向量的夹角公式即可求出法向量的夹角,从而求出二面角的大小.
解答: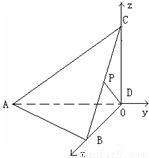 解:(I)如图,以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系.则
解:(I)如图,以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系.则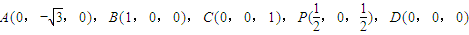 )
)
∴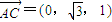 ,
,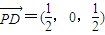
∴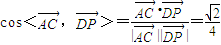
所以,异面直线AC与BD所成角的余弦值为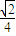
(II)面DAB的一个法向量为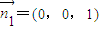
设面ABC的一个法向量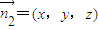 ,
,
则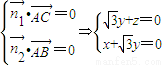 ,
,
取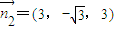 ,
,
则∴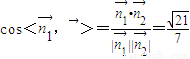
∴二面角C-AB-D的大小为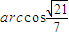
点评:本小题主要考查异面直线所成的角,以及空间向量和二面角等基础知识,考查空间想象能力、运算能力和推理论证能力,属于基础题.
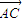 和
和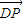 的坐标,利用向量的夹角公式即可求出所成角;
的坐标,利用向量的夹角公式即可求出所成角;(Ⅱ)要求二面角C-AB-D的大小,即分别求出两平面的法向量,然后利用向量的夹角公式即可求出法向量的夹角,从而求出二面角的大小.
解答:
 解:(I)如图,以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系.则
解:(I)如图,以D为坐标原点,DB、AD、DC所在直线分别为x,y,z轴建立直角坐标系.则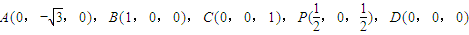 )
)∴
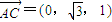 ,
,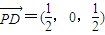
∴
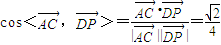
所以,异面直线AC与BD所成角的余弦值为
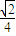
(II)面DAB的一个法向量为
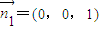
设面ABC的一个法向量
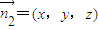 ,
,则
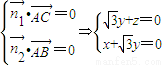 ,
,取
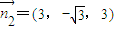 ,
,则∴
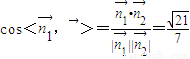
∴二面角C-AB-D的大小为
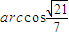
点评:本小题主要考查异面直线所成的角,以及空间向量和二面角等基础知识,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
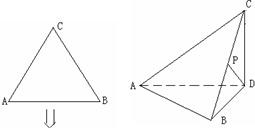 把边长为2的正三角形ABC沿BC上的高AD折成直二面角,设折叠后BC的中点为P,
把边长为2的正三角形ABC沿BC上的高AD折成直二面角,设折叠后BC的中点为P, 已知l1,l2,l3是同一平面内三条不重合自上而下的平行直线.
已知l1,l2,l3是同一平面内三条不重合自上而下的平行直线.
