题目内容
已知曲线y=1-x2上一点P（
，
），则过点P的切线的倾斜角为（ ）A．30°
B．45°
C．135°
D．150°
【答案】分析：先求出函数的导数y′的解析式，，再根据函数的导数就是函数在此点的切线的斜率，从而来求出倾斜角．
解答：解：y′=-2x，当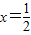
时，y′=-1，所以过点P的切线的倾斜角为135°
故选C
点评：本题考查函数的导数的几何意义，直线的倾斜角和斜率的关系．
解答：解：y′=-2x，当
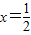时，y′=-1，所以过点P的切线的倾斜角为135°故选C
点评：本题考查函数的导数的几何意义，直线的倾斜角和斜率的关系．
练习册系列答案
相关题目
已知曲线y=1-x2上一点P（
，
），则过点P的切线的倾斜角为（ ）
| 1 |
| 2 |
| 3 |
| 4 |
| A、30° | B、45° |
| C、135° | D、150° |
，
），则过点P的切线的倾斜角为