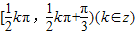题目内容
下列有六个命题:
(1)y=tanx在定义域上单调递增
(2)若向量
∥
,
∥
,则可知
∥
(3)函数y=4cos(2x+
)的一个对称点为(
,0)
(4)非零向量
、
满足|
+
|=|
-
|,则可知
•
=0
(5)tan(2x+
)≥
的解集为[
kπ,
kπ+
)(k∈z)
其中真命题的序号为
(1)y=tanx在定义域上单调递增
(2)若向量
| a |
| b |
| b |
| c |
| a |
| c |
(3)函数y=4cos(2x+
| π |
| 6 |
| π |
| 6 |
(4)非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
(5)tan(2x+
| π |
| 3 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 3 |
其中真命题的序号为
(3)(4)
(3)(4)
.分析:(1)由正切函数y=tanx的单调性即可判断出;
(2)当
=
时,不一定正确;
(3)满足cosx=0的点(x,0)都是函数y=cosx的对称点;
(4)由已知可得(
+
)2=(
-
)2,化简即可;
(5)解出比较即可.
(2)当
| b |
| 0 |
(3)满足cosx=0的点(x,0)都是函数y=cosx的对称点;
(4)由已知可得(
| a |
| b |
| a |
| b |
(5)解出比较即可.
解答:解:(1)我们知道:y=tanx在每个区间(-
+kπ,
+kπ)(k∈Z)单调递增,但是在整个定义域上不是单调函数,故不正确;
(2)若
≠
,
=
,
≠
,则
与
不一定共线,故不正确;
(3)∵4cos(2×
+
)=4cos
=0,∴点(
,0)是函数y=4cos(2x+
)的一个对称点,因此正确;
(4)∵非零向量
、
满足|
+
|=|
-
|,∴(
+
)2=(
-
)2,化为
•
=0,因此正确;
(5)∵tan(2x+
)≥
,∴kπ+
≤2x+
<
+kπ(k∈Z),解得
≤x<
+
(k∈Z),因此(5)不正确.
综上可知:真命题为(3)(4).
故答案为(3)(4).
| π |
| 2 |
| π |
| 2 |
(2)若
| a |
| 0 |
| b |
| 0 |
| c |
| 0 |
| a |
| c |
(3)∵4cos(2×
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
(4)∵非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
(5)∵tan(2x+
| π |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
| kπ |
| 2 |
综上可知:真命题为(3)(4).
故答案为(3)(4).
点评:熟练掌握三角函数的性质及向量的共线是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
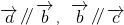 ,则可知
,则可知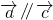
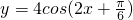 的一个对称点为
的一个对称点为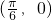
 、
、 满足
满足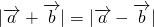 ,则可知
,则可知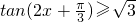 的解集为
的解集为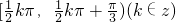
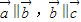 ,则可知
,则可知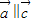
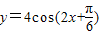 的一个对称点为
的一个对称点为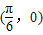
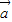 、
、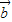 满足
满足 ,则可知
,则可知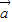 •
•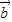 =0
=0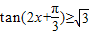 的解集为
的解集为