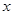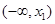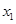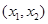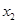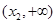题目内容
已知函数 .
.
(Ⅰ)当 时,求函数
时,求函数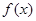 的极值;
的极值;
(Ⅱ)若函数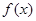 的图象与x轴有三个不同的交点,求a的取值范围。
的图象与x轴有三个不同的交点,求a的取值范围。
【答案】
解:(1)当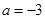 时,
时,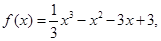 ∴
∴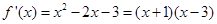 。
。
令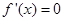 ,得
,得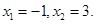 当
当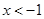 时,
时,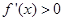 ,则
,则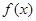 在
在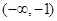 上单调递增;
上单调递增;
当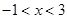 时,
时,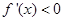 ,则
,则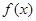 在
在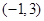 上单调递减;当
上单调递减;当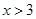 时,
时,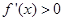 ,则
,则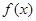 在
在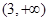 上单调递增; ∴当
上单调递增; ∴当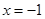 时,
时,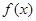 取得极大值为
取得极大值为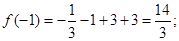
当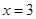 时,
时,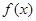 取得极小值为
取得极小值为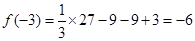 。
。
(2)∵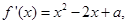 ∴
∴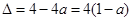 。
。
若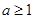 ,则
,则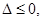
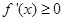 在R上恒成立,则
在R上恒成立,则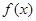 在R上单调递增;函数
在R上单调递增;函数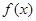 的图象与轴有且只有一个交点,不合题意。
的图象与轴有且只有一个交点,不合题意。
若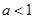 ,则
,则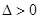 ,
, 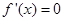 有两个不相等的实根,不妨设为
有两个不相等的实根,不妨设为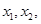 且
且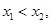
则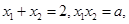
当x变化时,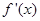 ,
,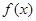 的取值情况如下表:
的取值情况如下表:
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
↗ |
极大值 |
↘ |
极小值 |
↗ |
∵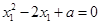 ,∴
,∴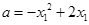 ,
,
∴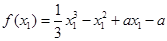
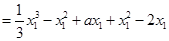
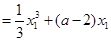
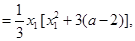
同理,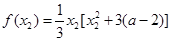 。∴
。∴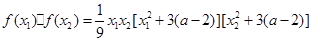
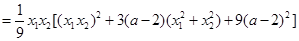
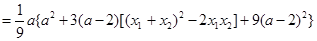
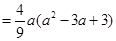 ,令
,令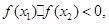
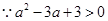
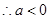
此时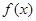 的图象与x轴有三个不同的交点。综上所述,a的取值范围是
的图象与x轴有三个不同的交点。综上所述,a的取值范围是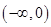
【解析】略

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目