题目内容
已知函数f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1.
(1)求f(9),f(27)的值;
(2)求f(
)+f(
)+f(
)+f(2)+f(3)+f(4)的值;
(3)解不等式:f(x)+f(x-8)<2.
(1)求f(9),f(27)的值;
(2)求f(
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
(3)解不等式:f(x)+f(x-8)<2.
分析:(1)由函数f(x)在定义域(0,+∞)上为增函数,且满足f(xy)=f(x)+f(y),f(3)=1,能求出f(9)和f(27).
(2)令x=y=1,则f(1)=f(1)+f(1)=2f(1),知f(1)=0,令y=
,则f(x•
)=f(x)+f(
)=0,由此能求出f(
)+f(
)+f(
)+f(2)+f(3)+f(4).
(3)由f(x)+f(x-8)<2,知f(x)+f(x-8)=f[x(x-8)]<f(9),再由函数f(x)在定义域(0,+∞)上为增函数,能求出原不等式的解集.
(2)令x=y=1,则f(1)=f(1)+f(1)=2f(1),知f(1)=0,令y=
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
(3)由f(x)+f(x-8)<2,知f(x)+f(x-8)=f[x(x-8)]<f(9),再由函数f(x)在定义域(0,+∞)上为增函数,能求出原不等式的解集.
解答:解:(1)∵函数f(x)在定义域(0,+∞)上为增函数,
且满足f(xy)=f(x)+f(y),f(3)=1,
∴f(9)=f(3)+f(3)=2,
f(27)=f(9)+f(3)=2+1=3.…(2分)
(2)令x=y=1,则f(1)=f(1)+f(1)=2f(1),
∴f(1)=0,
令y=
,则f(x•
)=f(x)+f(
)=f(1)=0,…(4分)
∴f(
)+f(
)+f(
)+f(2)+f(3)+f(4)
=f(
)+f(4)+f(
)+f(3)+f(
)+f(2)=0.…(7分)
(3)∵f(x)+f(x-8)<2,
∴f(x)+f(x-8)=f[x(x-8)]<f(9),…(9分)
而函数f(x)在定义域(0,+∞)上为增函数,
∴
,解得8<x<9,…(11分)
即原不等式的解集为(8,9).…(12分)
且满足f(xy)=f(x)+f(y),f(3)=1,
∴f(9)=f(3)+f(3)=2,
f(27)=f(9)+f(3)=2+1=3.…(2分)
(2)令x=y=1,则f(1)=f(1)+f(1)=2f(1),
∴f(1)=0,
令y=
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
∴f(
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
=f(
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
(3)∵f(x)+f(x-8)<2,
∴f(x)+f(x-8)=f[x(x-8)]<f(9),…(9分)
而函数f(x)在定义域(0,+∞)上为增函数,
∴
|
即原不等式的解集为(8,9).…(12分)
点评:本题考查抽象函数的函数值的求法,考查不等式的解法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
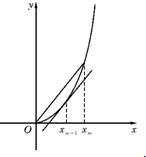 已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
已知函数f(x)=x3+x2,数列|xn|(xn>0)的第一项xn=1,以后各项按如下方式取定:曲线x=f(x)在(xn+1,f(xn+1))处的切线与经过(0,0)和(xn,f (xn))两点的直线平行(如图).
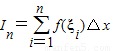 中ξi的选取是任意的,且In仅于n有关.
中ξi的选取是任意的,且In仅于n有关.