题目内容
15.根据下列条件解三角形.(1)已知:∠A=60°,∠B=45°,c=10.
(2)已知:a=4,b=5,c=6.
分析 (1)利用正弦定理,可解三角形;
(2)利用余弦定理,可解三角形.
解答 解:(1)∠C=180°-60°-45°=75°.
由正弦定理可得$\frac{a}{\frac{\sqrt{3}}{2}}=\frac{b}{\frac{\sqrt{2}}{2}}=\frac{10}{sin75°}$,
∴a=15$\sqrt{2}$-5$\sqrt{6}$,b=10$\sqrt{3}$-10;
(2)cosA=$\frac{25+36-16}{2×5×6}$=$\frac{3}{4}$,A=arccos$\frac{3}{4}$,
cosB=$\frac{16+36-25}{2×4×6}$=$\frac{9}{16}$,B=arccos$\frac{9}{16}$,
C=π-arccos$\frac{3}{4}$-arccos$\frac{9}{16}$.
点评 本题考查解三角形,考查正弦定理、余弦定理的运用,比较基础.

练习册系列答案
相关题目
4.二项式(x2-$\frac{1}{x}$)6的展开式中不含x3项的系数之和为( )
| A. | 20 | B. | 24 | C. | 30 | D. | 36 |
 如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.当水位上涨,水面宽为2米时,拱顶到水面的距离为0.5米.
如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.当水位上涨,水面宽为2米时,拱顶到水面的距离为0.5米.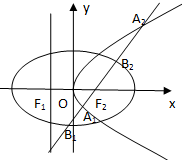 设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为$\frac{1}{2}$的椭圆记作C2
设抛物线C1:y2=4x的准线与x轴交于点F1,焦点为F2;以F1,F2为焦点,离心率为$\frac{1}{2}$的椭圆记作C2