题目内容
函数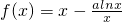 ,其中a为常数.
,其中a为常数.
(1)证明:对任意a∈R,函数y=f(x)图象恒过定点;
(2)当a=1时,不等式f(x)+2b≤0在x∈(0,+∞)上有解,求实数b的取值范围;
(3)若对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,求m的最小值.
(1)证明:令lnx=0,得x=1,且f(1)=1,
∴函数y=f(x)图象恒过定点(1,1). …(2分)
(2)解:当a=1时,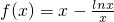 ,
,
∴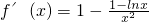 ,即
,即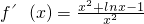 ,
,
令f'(x)=0,得x=1.
∴fmin(x)=f(1)=1,
∵f(x)+2b≤0在x∈(0,+∞)上有解,
∴-2b≥fmin(x),即-2b≥1,
∴实数b的取值范围为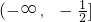 .…(9分)
.…(9分)
(3)解: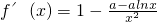 ,即
,即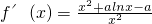 ,令g(x)=x2+alnx-a,
,令g(x)=x2+alnx-a,
由题意可知,对任意a∈[m,0),f'(x)≥0在x∈(0,+∞)恒成立,
即h(x)=x2+alnx-a≥0在x∈(0,+∞)恒成立.
∵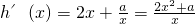 ,令h'(x)=0,得
,令h'(x)=0,得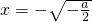 (舍)或
(舍)或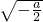 .
.
列表如下:
∴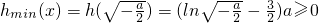 ,解得a≥-2e3.
,解得a≥-2e3.
∴m的最小值为-2e3. …(16分)
分析:(1)令lnx=0,得x=1,且f(1)=1,由此可得结论;
(2)利用f(x)+2b≤0在x∈(0,+∞)上有解,可得-2b≥fmin(x),求出函数的最小值,即可求实数b的取值范围;
(3)对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,等价于对任意a∈[m,0),f'(x)≥0在x∈(0,+∞)恒成立,即h(x)=x2+alnx-a≥0在x∈(0,+∞)恒成立,由此可得结论.
点评:本题考查导数知识的运用,考查函数的最值,考查恒成立问题,确定函数的最值是关键.
∴函数y=f(x)图象恒过定点(1,1). …(2分)
(2)解:当a=1时,
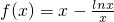 ,
,∴
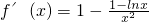 ,即
,即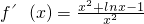 ,
,令f'(x)=0,得x=1.
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 极小值 |
∵f(x)+2b≤0在x∈(0,+∞)上有解,
∴-2b≥fmin(x),即-2b≥1,
∴实数b的取值范围为
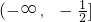 .…(9分)
.…(9分)(3)解:
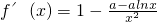 ,即
,即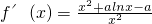 ,令g(x)=x2+alnx-a,
,令g(x)=x2+alnx-a,由题意可知,对任意a∈[m,0),f'(x)≥0在x∈(0,+∞)恒成立,
即h(x)=x2+alnx-a≥0在x∈(0,+∞)恒成立.
∵
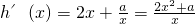 ,令h'(x)=0,得
,令h'(x)=0,得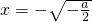 (舍)或
(舍)或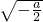 .
.列表如下:
| x | (0,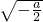 ) ) | 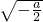 | (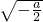 ,+∞) ,+∞) |
| h'(x) | - | 0 | + |
| h(x) | ↘ | 极小值 | ↗ |
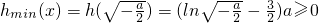 ,解得a≥-2e3.
,解得a≥-2e3.∴m的最小值为-2e3. …(16分)
分析:(1)令lnx=0,得x=1,且f(1)=1,由此可得结论;
(2)利用f(x)+2b≤0在x∈(0,+∞)上有解,可得-2b≥fmin(x),求出函数的最小值,即可求实数b的取值范围;
(3)对任意a∈[m,0)时,函数y=f(x)在定义域上恒单调递增,等价于对任意a∈[m,0),f'(x)≥0在x∈(0,+∞)恒成立,即h(x)=x2+alnx-a≥0在x∈(0,+∞)恒成立,由此可得结论.
点评:本题考查导数知识的运用,考查函数的最值,考查恒成立问题,确定函数的最值是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
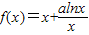 ,其中a为常数.
,其中a为常数. ,其中a为常数.
,其中a为常数.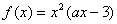 ,其中a为常数。
,其中a为常数。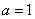 ,求:
,求: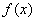 的图象在点
的图象在点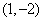 处的切线方程;
处的切线方程;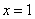 是函数
是函数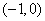 上是增函数,求:实数a的取值范围。
上是增函数,求:实数a的取值范围。