题目内容
有以下五个命题①y=sin2x+
的最小值是6.②已知f(x)=
,则f(4)<f(3).③函数f(x)值域为(-∞,0],等价于f(x)≤0恒成立.④函数y=
在定义域上单调递减.⑤若函数y=f(x)的值域是[1,3],则函数F(x)=1-f(x+3)的值域是[-5,-3].其中真命题是:
| 9 |
| sin2x |
x-
| ||
x-
|
| 1 |
| x-1 |
③
③
.分析:①利用均值不等式进行放缩,注意取等号的条件;
②对f(x)进行求导,利用导数判断f(x)的增减性,从而进行判断;
③根据函数值域的定义进行判断;
④可以类比于反比例函数,对其进行判断;
⑤本题只是自变量x发生了变化,函数值y并未随之发生变化,可知f(x)与f(x+3)的值域一样,利用此信息进行求解;
②对f(x)进行求导,利用导数判断f(x)的增减性,从而进行判断;
③根据函数值域的定义进行判断;
④可以类比于反比例函数,对其进行判断;
⑤本题只是自变量x发生了变化,函数值y并未随之发生变化,可知f(x)与f(x+3)的值域一样,利用此信息进行求解;
解答:解:①∵y=sin2x+
≥2
=6,当sin2x=
时等号成立,即sin2x=3,∵sin2x≤1,取不到等号,所以函数y的最小值取不到6,故①错误;
②f(x)=
对其进行求导可得:f′(x)=
>0,在(-∞,
),(
,+∞)上是增函数,
∴f(3)<f(4),故②错误;
③函数f(x)值域为(-∞,0],可以说明f(x)≤0,故③正确;
④函数y=
在定义域为{x|x≠1},在(-∞,1)和(1,+∞)上是减函数,
不能说在整个定义域上为减函数,故④错误;
⑤函数y=f(x)的值域是[1,3],可得y=f(x+3)的定义域为[1,3],
∴-2≤1-f(x+3)≤0,∴函数F(x)=1-f(x+3)的值域是[-2,0],故⑤错误;
∴③正确;
故答案为:③;
| 9 |
| sin2x |
| 9 |
| 9 |
| sin2x |
②f(x)=
x-
| ||
x-
|
| ||||
(x-
|
| 10 |
| 10 |
∴f(3)<f(4),故②错误;
③函数f(x)值域为(-∞,0],可以说明f(x)≤0,故③正确;
④函数y=
| 1 |
| x-1 |
不能说在整个定义域上为减函数,故④错误;
⑤函数y=f(x)的值域是[1,3],可得y=f(x+3)的定义域为[1,3],
∴-2≤1-f(x+3)≤0,∴函数F(x)=1-f(x+3)的值域是[-2,0],故⑤错误;
∴③正确;
故答案为:③;
点评:注意函数图象左右平移只是改变;自变量x的取值,函数的值域并不改变,此题主要考查均值不等式的利用以及利用导数研究函数的单调性,考查的知识点比较多,是一道综合题;

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
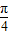 ],则点P到曲线y=f(x)对称轴距离的取值范围为[0,
],则点P到曲线y=f(x)对称轴距离的取值范围为[0, ];
];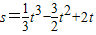 ,那么速度为零的时刻只有1秒末;
,那么速度为零的时刻只有1秒末; 内单调递增,则a的取值范围是
内单调递增,则a的取值范围是 ;
; 的最小值是6.②已知
的最小值是6.②已知 ,则f(4)<f(3).③函数f(x)值域为(-∞,0],等价于f(x)≤0恒成立.④函数
,则f(4)<f(3).③函数f(x)值域为(-∞,0],等价于f(x)≤0恒成立.④函数 在定义域上单调递减.⑤若函数y=f(x)的值域是[1,3],则函数F(x)=1-f(x+3)的值域是[-5,-3].其中真命题是: .
在定义域上单调递减.⑤若函数y=f(x)的值域是[1,3],则函数F(x)=1-f(x+3)的值域是[-5,-3].其中真命题是: .