题目内容
若不等式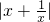
＞|a-2|+1对于一切非零实数x均成立，则实数a的取值范围是________．
（1，3）
分析：由题意求出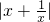的最小值，只要|a-2|+1小于最小值，即可满足题意，求出a的范围即可．
解答：∵x与
同号，∴
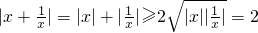．（当且仅当x=±1时取“=”）
∴2＞|a-2|+1．∴|a-2|＜1，解得1＜a＜3．
故答案为：（1，3）
点评：本题考查绝对值不等式的解法，恒成立问题一般通过函数的最值解决，注意端点问题的处理．是高考常考题．
分析：由题意求出
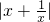的最小值，只要|a-2|+1小于最小值，即可满足题意，求出a的范围即可．解答：∵x与
同号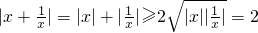，∴．（当且仅当x=±1时取“=”）∴2＞|a-2|+1．∴|a-2|＜1，解得1＜a＜3．
故答案为：（1，3）
点评：本题考查绝对值不等式的解法，恒成立问题一般通过函数的最值解决，注意端点问题的处理．是高考常考题．
练习册系列答案
相关题目