Question

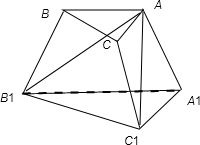
三棱台ABC-A₁B₁C₁中，上底面ABC的面积为a²，下底面面积为b²（b＞a＞0），作截面AB₁C₁，设直线BC与平面AB₁C₁的距离等于这个三棱台的高，那么截面AB₁C₁的面积是（　　）

• A、

  1

  3

  ab
• B、ab
• C、3ab
• D、

  1

  3

  (a+b)2

Answer 1

分析：连接BC₁后，我们可以将三棱台ABC-A₁B₁C₁体积分为三个三棱锥的体积之和，根据已知中上底面ABC的面积为a²，下底面面积为b²（b＞a＞0），直线BC与平面AB₁C₁的距离等于这个三棱台的高，结合棱台和棱锥体积公式即可得到截面AB₁C₁的面积．

解答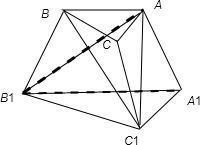：解：连接BC₁，如下图所示：
设三棱台的高为h，
则VABC-A1B1C1=

1

3

(SABC+

SABC•SA1B1C1

+SA1B1C1)h
=VABC-A1+VA-A1B1C1+VB-A B1C1
=

1

3

SABCh+

1

3

SA1B1C1h+

1

3

SA B1C1h，
∴

SABC•SA1B1C1

=SA B1C1
又∵上底面ABC的面积为a²，下底面面积为b^{2
∴SA B1C1}=ab
故选B

点评：本题考查的知识点是棱台的体积公式和棱锥的体积公式，将棱台的体积VABC-A1B1C1分成三个三棱锥VABC-A1+VA-A1B1C1+VB-A B1C1的体积和，是解答本题的关键．