题目内容
在三棱台A1B1C1—ABC中,侧棱BB1⊥底面ABC,且∠ABC=∠AA1C=90°,AB=2A1B1=2cm.
(1)求证:BC⊥A1B1,BC⊥A1A1,AA1⊥A1B;
(2)求异面直线AA1和BC的距离.
答案:
解析:
解析:
证明:(1)
∵ B1B⊥平面ABC,∴ B1B⊥BC, 又BC⊥AB,∴ BC⊥平面B1BAA1, 故A1B是斜线A1C在面A1B内的射影. ∵ AA1⊥A1C. ∴ 由三垂线定理AA1⊥A1B, ∵ AA1C平面A1B.∴ BC⊥A1A.BC⊥A1B. (2)∵ AA1⊥A1B,BC⊥A1B.∴ A1B即为异面直线的距离. ∵ ∴ ∴ 即AA1到BC的距离为
|

练习册系列答案
相关题目

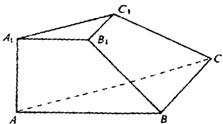 如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A=A1B1=B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45°,求这个棱台的体积.
如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A=A1B1=B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45°,求这个棱台的体积. 如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A= A1B1= B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45??,求这个棱台的体积.
如图,在三棱台A1B1C1-ABC中,已知A1A⊥底面ABC,A1A= A1B1= B1C1=a,B1B⊥BC,且B1B和底面ABC所成的角45??,求这个棱台的体积.