题目内容
已知a≠b,且a2+2a-1=0,b2+2b-1=0,则代数式
+
=( )
| 1 |
| a |
| 1 |
| b |
分析:a2+2a=1,b2+2b=1,且a和b是一元二次方程 x2+2x-1=0 的两个根,故有 a+b=-2,由此求得
+
=
+
=2+2+( a+b)的值.
| 1 |
| a |
| 1 |
| b |
| a2+2a |
| a |
| b2+2b |
| b |
解答:解:∵已知a≠b,且a2+2a-1=0,b2+2b-1=0,
∴a2+2a=1,b2+2b=1,且a和b是一元二次方程 x2+2x-1=0 的两个根,
故 a+b=-2,
∴
+
=
+
=2+2+( a+b)=2,
故选B.
∴a2+2a=1,b2+2b=1,且a和b是一元二次方程 x2+2x-1=0 的两个根,
故 a+b=-2,
∴
| 1 |
| a |
| 1 |
| b |
| a2+2a |
| a |
| b2+2b |
| b |
故选B.
点评:本题主要考查一元二次方程根的分布与系数的关系,判断a和b是一元二次方程 x2+2x-1=0 的两个根,是解题的关键,属于中档题.

练习册系列答案
相关题目
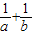 =( )
=( )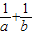 =( )
=( )