题目内容
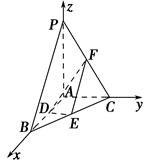
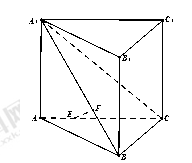
在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D,E,F分别是棱AB,BC,CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为________.
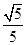
以A为原点,AB,AC,AP所在直线分别为x轴、y轴、z轴建立空间直角坐标系,由AB=AC=1,PA=2,得A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2),D( ,0,0),E
,0,0),E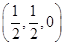 ,F
,F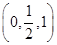 ,
,
∴ =(0,0,2),
=(0,0,2),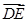 =
= ,
,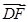 =
=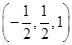 ,设面DEF的法向量为n=(x,y,z).
,设面DEF的法向量为n=(x,y,z).
则由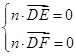 得
得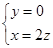 取z=1,则n=(2,0,1),设PA与平面DEF所成角为θ,则sin θ=
取z=1,则n=(2,0,1),设PA与平面DEF所成角为θ,则sin θ= =
=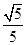 .
.
 ,0,0),E
,0,0),E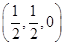 ,F
,F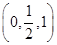 ,
,
∴
 =(0,0,2),
=(0,0,2),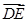 =
= ,
,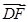 =
=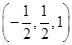 ,设面DEF的法向量为n=(x,y,z).
,设面DEF的法向量为n=(x,y,z).则由
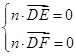 得
得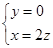 取z=1,则n=(2,0,1),设PA与平面DEF所成角为θ,则sin θ=
取z=1,则n=(2,0,1),设PA与平面DEF所成角为θ,则sin θ= =
=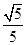 .
.
练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 (侧棱和底面垂直的棱柱)中,
(侧棱和底面垂直的棱柱)中,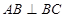 ,
,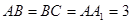 ,
,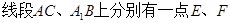 ,且满足
,且满足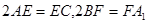 .
.
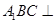 侧面
侧面 ;
; 的平面角的余弦值。
的平面角的余弦值。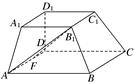
 AD,CD
AD,CD
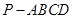 的底面
的底面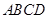 为一直角梯形,侧面PAD是等边三角形,其中
为一直角梯形,侧面PAD是等边三角形,其中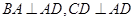 ,
,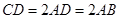 ,平面
,平面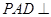 底面
底面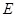 是
是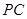 的中点.
的中点.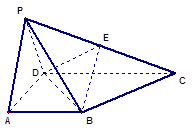
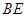 //平面
//平面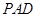 ;
;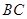 与平面BDE所成角的余弦值;
与平面BDE所成角的余弦值;


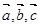 不共线,且两两之间的夹角都相等,若
不共线,且两两之间的夹角都相等,若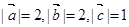 ,则
,则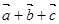 与
与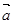 的夹角是 ▲ .
的夹角是 ▲ .