题目内容
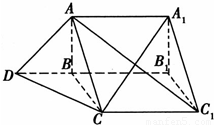
 如图所示,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC,AB=
如图所示,放置在水平面上的组合体由直三棱柱ABC-A1B1C1与正三棱锥B-ACD组成,其中,AB⊥BC,AB=| 2 |
(1)求直线CA1与平面ACD所成角的正弦值;
(2)在线段AC1上是否存在点P,使B1P⊥平面ACD?若存在,确定点P的位置;若不存在,请说明理由.
分析:(1)以点B为原点,分别以BC、BB1、BA为x轴、y轴、z轴建立空间直角坐标系,求出平面ACD的法向量,进而可利用夹角公式求出直线CA1与平面ACD所成角的正弦;
(2)假设存在,令
=m
=(
m,2m,-
m),利用
∥
,即可得到结论.
(2)假设存在,令
| AP |
| AC1 |
| 2 |
| 2 |
| B1P |
| n |
解答: 解:(1)由题意,AB⊥平面BB1C1C,CD?平面BB1C1C,
解:(1)由题意,AB⊥平面BB1C1C,CD?平面BB1C1C,
∴D,B,B1三点共线,
∵三棱锥是正三棱锥,
∴AB=BC=BD,
以点B为坐标原点,射线BC,BB1,BA分别为x,y,z轴,建立空间直角坐标系,则A(0,0,
),C(
,0,0),D(0,-
,0),B1(0,2,0),C1(
,2,0),A1(0,2,
)
设直线CA1与平面ACD所成角为θ
∵△ACD的重心G(
,-
,
),∴
=(
,-
,
),
∴取
=(1,-1,1)为平面ACD的法向量
∵
=(-
,2,
),
∴取
=(1,-
,-1)为直线CA1的方向向量
∴sinθ=|cos<
,
>|=
=
=
;
(2)令
=m
=(
m,2m,-
m),
则
=
+
=(
m,2m-2,
-
m)
∵
∥
,∴
=λ
∴
,无解
∴不存在满足条件的点P.
 解:(1)由题意,AB⊥平面BB1C1C,CD?平面BB1C1C,
解:(1)由题意,AB⊥平面BB1C1C,CD?平面BB1C1C,∴D,B,B1三点共线,
∵三棱锥是正三棱锥,
∴AB=BC=BD,
以点B为坐标原点,射线BC,BB1,BA分别为x,y,z轴,建立空间直角坐标系,则A(0,0,
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
设直线CA1与平面ACD所成角为θ
∵△ACD的重心G(
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| BG |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
∴取
| n |
∵
| CA1 |
| 2 |
| 2 |
∴取
| m |
| 2 |
∴sinθ=|cos<
| m |
| n |
| ||||
|
|
| ||
2
|
| ||
| 6 |
(2)令
| AP |
| AC1 |
| 2 |
| 2 |
则
| B1P |
| B1A |
| AP |
| 2 |
| 2 |
| 2 |
∵
| B1P |
| n |
| B1P |
| n |
∴
|
∴不存在满足条件的点P.
点评:本题以组合体为载体,考查线面角,考查线面垂直,关键是构建空间直角坐标系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
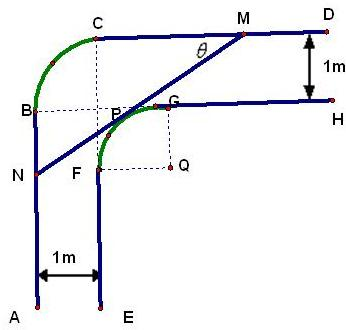 一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.
一走廊拐角下的横截面如图所示,已知内壁FG和外壁BC都是半径为1m的四分之一圆弧,AB,DC分别与圆弧BC相切于B、C两点,EF∥AB,GH∥CD,且两组平行墙壁间的走廊宽度都是1m.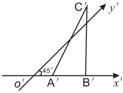 如图所示,△A′B′C′表示水平放置的△ABC在斜二测画法下的直观图,A′B′在x′轴上,B′C′与x′轴垂直,且B′C′=3,则△ABC的边AB上的高为( )
如图所示,△A′B′C′表示水平放置的△ABC在斜二测画法下的直观图,A′B′在x′轴上,B′C′与x′轴垂直,且B′C′=3,则△ABC的边AB上的高为( ) 如图所示,△A′O′B′表示水平放置的△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=2,则△AOB的边OB上的高为
如图所示,△A′O′B′表示水平放置的△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=2,则△AOB的边OB上的高为 ,BB1=2.
,BB1=2.