题目内容
(本题满分12分)
一个四棱椎的三视图如图所示:(I)求证:PA⊥BD;
(II)在线段PD上是否存在一点Q,使二面角Q-AC-D的平面角为30o?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】
(I)由三视图可知P-ABCD为四棱锥,底面ABCD为正方形,且PA=PB=PC=PD,
连接AC、BD交于点O,连接PO . ……………………………………………3分
因为BD⊥AC,BD⊥PO,所以BD⊥平面PAC,
即BD⊥PA.…………………………………………………………………………6分
(II)由三视图可知,BC=2,PA=2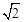 ,假设存在这样的点Q,
,假设存在这样的点Q,
因为AC⊥OQ,AC⊥OD,
所以∠DOQ为二面角Q-AC-D的平面角, ……………………………………8分
在△POD中,PD=2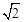 ,OD=
,OD=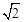 ,则∠PDO=60o,
,则∠PDO=60o,
在△DQO中,∠PDO=60o,且∠QOD=30o.所以DP⊥OQ. ……………10分
 所以OD=
所以OD=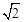 ,QD=
,QD=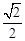 .
.
所以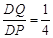 .
…………………………………………12分
.
…………………………………………12分
【解析】略

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面